Operating conditions for the cavity

The two previous sections have shown that a laser beam can be considered as a “concentrated spatial and spectral beam of light” and that the optical cavity plays a very important role. However, there are several conditions that must be fulfilled if the laser is to operate successfully. These involve the gain and loss of the cavity and the frequency.

The effective gain of an amplifying medium is defined by the ratio between the power of the outgoing beam Pout and the incoming beam Pin:

These two powers (expressed in watts or photons per second) refer to the beam before and after it passes through the amplifying medium (Figure 13).

Reflection coefficients can also be defined for the mirrors in the cavity (R1 and R2), supposing that the only loss of power is due to the reflections off these mirrors (Figure 14).

When the laser is operating continuously, the output power is constant despite the fact that the number of photons in the cavity increases when passing through the amplifying medium then decreases when reflected off the mirrors. Thus, the number of photons gained is equal to the number of photons lost.

P is the power of the laser just before the mirror M1. The power after a round trip is given by:

where G+ and G- are the effective gains in the positive (outgoing laser beam) and negative (incoming) directions, respectively.

It is necessary to distinguish the effective gains according to the direction of the wave propagation as this depends on the incident power, which is not the same in both directions (the reflection coefficients of the mirrors are different).

When the laser emits continuously, 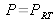so the product

If 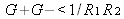, the laser cannot oscillate.

If 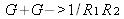, the power of the beam in the cavity increases each time. This increase is not infinite as the number of excited-state atoms is given by the pumping so the number of stimulated photons is finite. Thus, if the maximum number of photons that can be pumped per second is N, the effective gain can be defined by the formula where 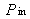is the power of the beam just before the amplifying medium (in photons per second). If 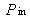increases, the effective gain decreases and tends towards 1. This phenomenon is known as gain saturation. Thus, when the power in the cavity increases significantly, 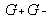decreases and finally stabilises at .

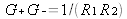The cavity mirrors must therefore be chosen so that 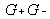is always more than 1 or, in other words, so that the gain is always greater than the loss in the cavity (represented by the transmissions of the mirrors).

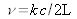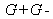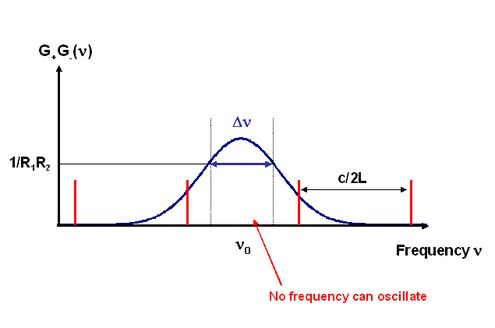
The various frequencies that can exist in the cavity are defined by the formula . They must also be situated in the bandwidth of the amplifying medium. In fact, the product has a certain bandwidth depending on the nature of the medium (for example, the helium-neon laser has a bandwidth of about 1 GHz). This means there is a certain spectral range defined by 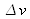where the frequencies will oscillate. These conditions of gain and frequency can be correlated graphically (Figure 15).

In the frequency comb imposed by the cavity, only those frequencies that meet the above conditions can lead to a laser oscillation. The others cannot exist. Generally, 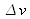is greater than 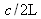. This means that quite a large number of frequencies will be able to oscillate (tens to hundreds of frequencies). The actual number depends on the bandwidth defined by 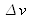and the spectrum imposed by the Fabry-Pérot cavity .

However, in some cases, is smaller than 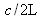(Figure 16). This often happens when the amplifying medium emits in a very narrow band (in CO2 lasers for example) or when the optical cavity is very small (microchip lasers have a cavity smaller than 1 mm). As a result, no frequency may be able to oscillate so the length of the cavity must be adjusted so that the laser can work.