Gaussian beams focusing and mode matching
A very common experimental action is to modify a Gaussian beam with a lens. For example, if one want to inject a given pump laser beam in another laser cavity, it is crucial that the beam “matches” the resonator of this last laser.
When passing through a lens, a Gaussian beam is turned into another Gaussian beam : let's see how.
By using the ABCD law (see corresponding paragraph) applied to a centred optical system (with the focal point set as the origin), one can find the relations between positions and sizes of the waists before and after the optical system.
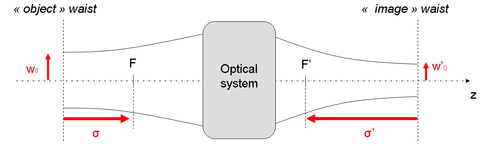
The “object waist” wo is located at the abscissa
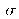relatively to the object focal point, whereas the “image waist” w'o is located at the absciss
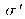with respect to the image focal point (see figure 13).
The notion of “object” and “image” waist is in fact not rigorously applicable here, because those two points are not conjugated. In other terms, the waist of the image beam is not the image of the waist of the object beam. We will nevertheless conserve this practical notation in the following.
The complex radius of curvature corresponding to the object waist is imaginary :
The transfer matrix elements of the optical system are (check it !):
![[zoom...]](javascript:window.open(%22../res/fig13_2.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
By applying the ABCD law, and using the fact that qo and q'o are both imaginary, we find the following relations :
or in a different form :
Those relations show that the position of the image waist depend not only on the position of the objetc waist, but also on its size. In the same way, the size of the image waist is a function of the size and position of the object waist.
-
When
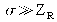, the waive around the focal point is nearly spherical (far field). From the lens point of view, the wave seems to come from a single point, and we have
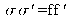. This is the Newton conjugation relation we used to see in classical geometric optics.
-
Another special case is
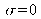, that is the object waist is located on the focal point of the lens. In ray optics, we expect a collimated beam (parallel rays) after the lens. With Gaussian beams, we have
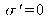: the image waist is located on the image focal point.
It is clear that the “conjugation relations” are very different in classical or Gaussian optics, especially around the focal points. However, we have to remind that the term “conjugation relation” has not the same meaning here and in geometric optics.
The relation of magnification between waists is given in this case by :
This relation is very important from the experimental point of view. Indeed, this is a very common configuration (focusing/collimation or the opposite). This relation gives a good order of magnitude to answer the following question : “what will be the size of the laser spot after focusing a nearly collimated beam with a lens (focal length f) ?”
![[zoom...]](javascript:window.open(%22../res/fig14_2.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
![[zoom...]](javascript:window.open(%22../res/fig15_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
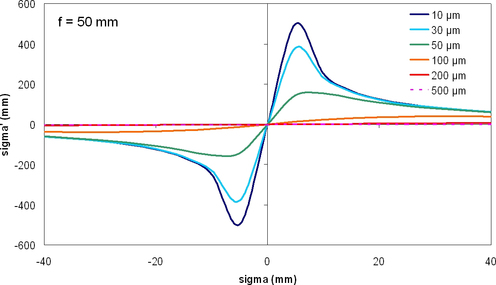
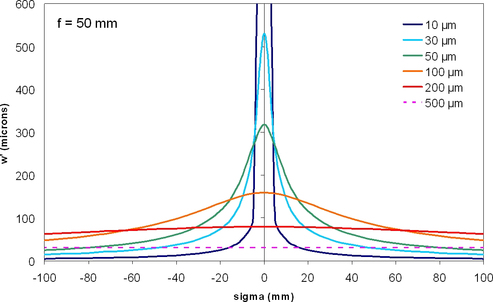
After observation of the figures 14 and 15 (illustrating the equations above), one can make the following comments :
-
On the figure 14, when the size of the object waist is large, we have
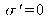for every value of
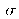: this is the geometric optics case, when a collimated beam is focused in the focal plan of a lens. The position of the object waist is not well-defined here as the Rayleigh distance is very big (“collimation” for large values of w).
-
When the object waist size is very small, the observed behaviour is also similar to geometric optics, with asymptotic limits given by
.
-
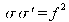Besides those two cases, the difference with geometric optics is huge : for w0 =10 µm and
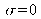small object waist located in the focal plane of the lens), the image waist is in the image focal plane, and not positioned to infinity as we learn from ray optics!
-
This “paradox” is explained by the figure 15 : for w0 =10 µm and
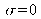, the image waist is actually in the image focal plane but its size is very big : the beam is quasi-collimated and we find a behaviour similar to what is expected from geometric optics.