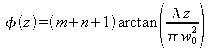Hermite-Gaussian Modes

Let's start with the modes having a rectangular geometry in a Cartesian coordinates system.

We can then write a solution of the wave equation as follows :

where g (respectively h) is a function of z and x (respectively z and y).

The insertion of this solution inside the paraxial wave equation leads to a differential equation for g and h : the solutions of this equation are Hermite's polynomials.

One can show (not demonstrated here) than a complete set of solutions is :

where :

• m, n are integers

• q, R et w were already defined for Gaussian beams (no change)

• 

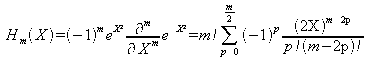• :m-order Hermite ploynomials

• As an example : H0(X) = 1, H1(X) = 2X, H2(X) = 4X²-2 etc.

• For m = n = 0, we have the fundamental Gaussian beam.

• For any m and n, the propagation law for R, q and w remains the same. Only the phase shift and the transverse beam structure differ.

The figures 19 and 20 depict the intensity pattern for those modes. One can notice some “zeros” for the intensity (dark lines) : their number correspond to the order m.

The phase-shift after one round trip in a two mirrors resonator has to be equal to p times (p is an integer). Starting from the phase expression 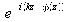and using the same method as in paragraph “ TEM00 mode frequencies” we obtain the following expression for the frequency of the TEMmnq mode:

gi = 1-d/Ri was previously defined for a two-mirrors cavity (length d, radius of curvature R). m=n=0 of course leads to the same expression as before for the fundamental Gaussian beam.

The frequencies depend on the values of the radii of curvature :

• For an almost plano-plano configuration (R1 = R2 >> d) :

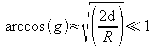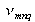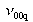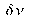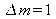The arccos term becomes arccos (g) and g is almost 1 so  : . The frequencies are very close from frequencies. The spectral intervalle for or 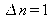is equal to 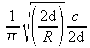(around some tens of MHz).

• For a quasi-confocal symmetrical resonator (R1 = R2 = d) the spectral gap between consecutive modes is c/4d and the frequencies are degenerated (a longitudinal mode and some transverse modes have the same frequencies).