Optical resonators and Gaussian beams

Stability

Let us write the ABCD matrix for a round trip,

which could be broke up as follows (see figure 2) :

  • a first path in air, over a distance L

  • a path in the crystal (refractive index n) over a distance l

  • The reflection on the plane mirror (no impact on the calculation)

  • Again, one path in the crystal and another in air.

  • Finally the reflection on the output coupler (radius of curvature R)

Figure 2 : scheme of the resonator
Figure 2 : scheme of the resonator [zoom...]Info

The unfolded cavity is presented in the figure 3 and correspond to the following sequence of matrices (the order is important !):

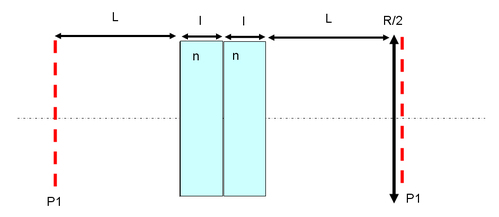
Figure 3 : unfolded cavity
Figure 3 : unfolded cavity [zoom...]

with d = L + l/n to make the notations lighter, we find after simple calculations :

The resonator is stable if or :

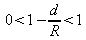as d/R is obviously positive so the condition reduces to :

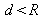soit en reprenant les notations de base

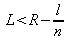
For an “empty” cavity (without crystal), with a length Leq, the stability condition was defined in the course as . As 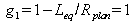because Rplan is equal to infinity, the condition becomes 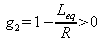or .

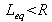From the stability point of view, the real cavity with the crystal is then equivalent to an empty cavity with an equivalent length .

The equivalent length does not correspond to the optical length L+nl !

Let's go back to our resonator : any couple (radius of curvature R – length L) is suitable as soon as the condition 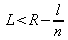is verified. From a practical point of view, other considerations such as the optimum size of the waist inside the crystal will impact this choice. Moreover, we generally do not have in the lab an infinite choice for the radii of curvature of the mirrors !

For the moment, let us pick in the lab a mirror with appropriate coatings and a radius of curvature R = 100 mm.

The length L must then be shorter than 100-10/1,8 ≈ 94,5 mm.

We will take for example in the following L = 80 mm.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Preliminary study of the hemispheric resonatorBeam profile inside the resonator