Optimisation of the cavity

We have obtained in the previous paragraph the characteristics of the beam for a specific value of L.

In most cases, the pumping conditions impose a given value for the waist, and consequently fix the resonator geometry, For example, in the course entitled “principles of lasers”, the pumping geometry (through the use of a 1 x 100 µm laser diode) leads to a fixed value for the pumping waist : it is focused in this specific case on a 20 x 100 µm spot. To simplify the calculations, we will here suppose that this spot is circular (which is the case when using fiber coupled laser diodes) with a 80 µm radius inside the laser crystal.

A crucial point is to match the laser mode with the pump mode size : we will try to get a laser mode size compatible with the pump spot size. More precisely, we will choose a laser mode slightly smaller than the pump mode, in order to benefit for an homogeneous pumping over all the laser mode area.

As an example, we will then try to have w0 = 60 µm.

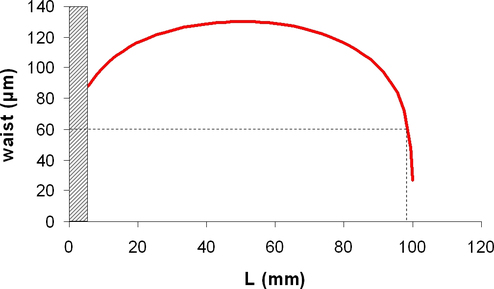
What is the length L in this case (always with our R=100 mm output coupler) ?

With the formula 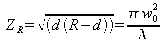, we get a trinomial :

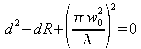Solving this trinomial gives two values for d :

d1 = 98,85 mm and d2 = 1,14 mm.

Of course only the first solution makes sense (for the other one, L is negative) and leads to L = 93,3 mm.

We are still in the stability zone, but near the frontier.

We can plot (figure 5) the evolution of the waist w with L for a given value of R (here 100 mm). Of course for L>R the resonator is unstable and we cannot define any waist.

There is a zone for L around R/2 = 50 mm where the waist stays almost constant. We also notice that with our output coupler, it is not possible to get a laser waist bigger than 130 µm. On the other hand, we can have very small waists near the stability limit.