Separable functions

A function of 2 independent variables is said to be separable if it can be expressed as a product of 2 functions, each of them depending on only one variable.

Example:

In polar coordinates:

These functions are easier to deal with because their two-dimensional FT simplifies in the product of 2 unidimensional FTs:

Those functions play an important role in optics where problems often exhibits this particular symmetry. A function g is of circular symmetry if it can be written, in polar coordinates, as a function of the only variable r:

We recall the FT definition:

To make use of the circular symmetry of g, we use planar polar coordinates in the planes (x,y) and (u,v):

In the general case, we have:

In polar coordinates, we can write:

consequently:

To cover the whole plane (x,y) with x and y ranging from 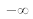  to 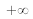, the double integral bounds become 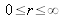and 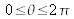. Therefore:

We define the Bessel function of first kind and zero order, J0(a), where a is a non-dimensional variable, by the following integral:

We can always choose the origin of angles in the plane (u,v) in order to obtain 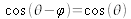; therefore equation (I-1) becomes:

By integrating this latter equation over r, we notice that 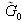depends only on .

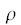This particular form of the FT is quite common in optics. We call it Fourier-Bessel transform or zero-order Hankel transform.

A similar demonstration shows that the inverse FT of a function with a circular symmetry 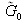can be expressed by:

Therefore, there is no difference between direct and inverse transforms for functions with circular symmetry. We use the notation B{ } to represent a Fourier-Bessel transform.