Interference signal

In the following example, let us consider two waves that are temporally and spatially coherent, and also coherently polarized. Given such a context, the observable signal is written simply as:

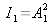The spatial dependence with is implied subsequently whenever possible. If we assume and , the interference signal is also written as [3]:

with:

where we take as the optical path difference between the waves. The interference signal is also called fringe pattern or interference pattern.

The interference phenomenon is indicated by alternating dark zones for which and bright zones for which 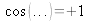. Taking 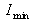as the minimum signal and 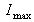as the maximum signal, we have:

We characterize the contrast of the fringe pattern by the visibility factor [3] :

The maximum contrast is equal to 1 and it is obtained for 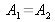, which means that both waves have the same amplitude for all points in space. If 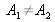, then the contrast is less than 1; and if or 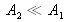, then we obtain .

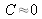The maxima for 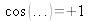occurs whenever:

The minima obtained for 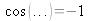, occurs whenever

The is referred to as the phase of the interferences. It consists of the difference between the optical phases of the waves, and it is proportional to a difference in optical paths.

The distance, at observation, which separates two consecutive zones of the same nature is referred to as the interfringe distance.

Figure 2 illustrates the properties of the interference signal.

We will now focus on two particular cases: when both waves are plane waves and when both waves are spherical waves.