Fabry-Perot Spectrometry

Fabry-Perot multiple waves interferometer can be used as a spectrometer. The experimental configuration is described in Figure 46. It is confocal Fabry-Perot: the mirrors are spherical with the same curvature beams and their focuses are confounded, the crater is stable so that the light can go back and forth to infinity staying around the optical axis.

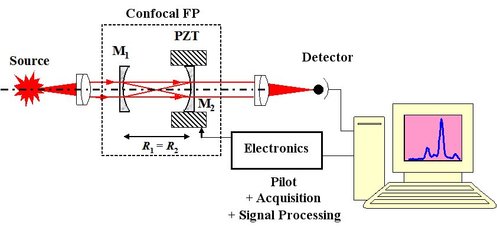
One of the mirrors is assembled on a piezoelectric transducer in order to make the crater thickness vary and to do a spectral scanning. The PZT pilot voltage is a ramp and for each spectrum frequency in phase with the crater instantaneous length the luminosity on the detector is maximal.

As an illustration, Figure 47 outlines the principle in the case of a multimode HeNe laser. Figure 47b shows the tension ramp that pilot the PZT and we can observe the laser spectrum in Figure 47a.

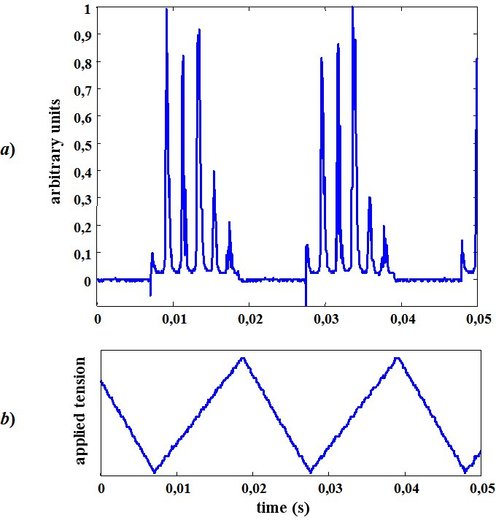
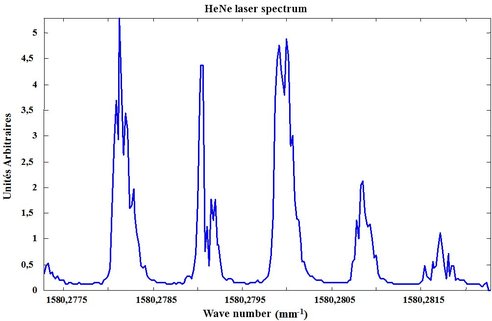
Figure 48 corresponds to a signal period observed in Figure 47a. The horizontal axis is given in a wave number by correspondence between the scale of frequency and the temporal one. Indeed, a period signal of Figure 47 corresponds to the Fabry-Perot free spectral interval.

The characteristics of that spectrometer are the following:

• Free spectral interval 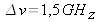namely

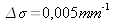
• Thinness

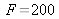
• Instrumental resolution 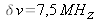namely

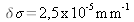
• Digital sampling 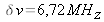namely

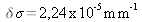
As the air cavity thickness made by both mirrors is 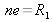,the spectrometer resolution power is given by (see Figure 18 for the notes):

It is proportional to the interferometer thinness and depends on the analyzed average wavelength

According to “Interferences: Fundamentals”, the degree of coherence is given by:

Where 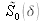is the Fourier transform 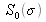, radiation spectral envelop.

The source coherent length can be estimated by:

Considering that the Fabry Perot spectrum measurement gives quantity 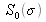, the degree of coherence is calculated by a discret Fourier transform of the measured spectrum. Figure 49 shows laser HeNe degree of coherence calculated from Figure 48 result.

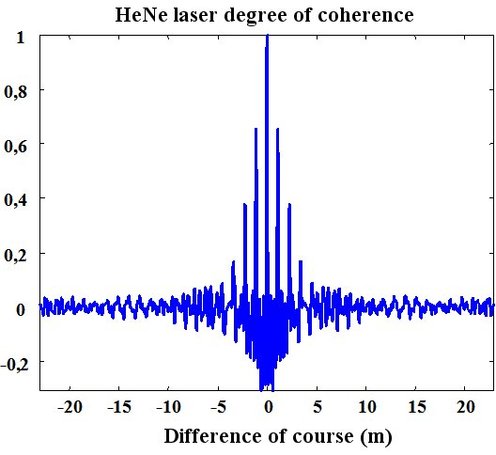
The coherence length computed with the degree of coherence is estimated as equal to .

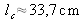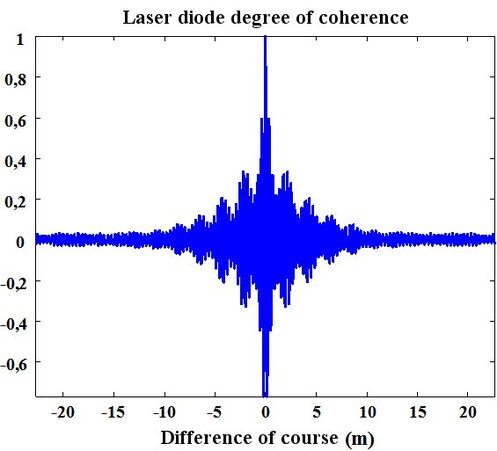
Another illustration is about a laser diode at 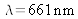which measured by the interferometer spectrum is illustrated in Figure 50.

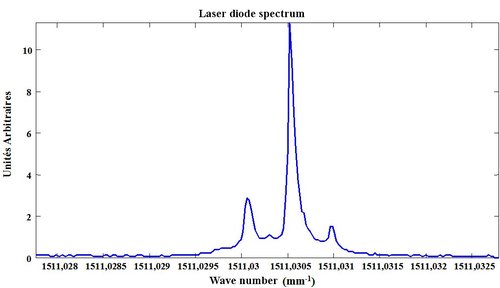
The laser diode degree of coherence is calculated by FFT and is represented in Figure 51. Its coherence length is estimated as equal to .
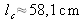