Recording a Hologram

Let's consider a stretched object lit by a monochromatic light wave, situated in the dimension with regards to the recording plane. This object diffracts a wave towards the observation plane situated at the distance of . The surface of the illuminated object generates a wave front that we observe as :

The amplitude describes the reflectivity of the object and the phase describes the surface appearance and its depth. Taking into account the results of the diffraction theory within the limits of the Fresnel conditions, the diffracted field at the dimension is expressed by an integral as follows :

Figure 1 illustrates the geometry of the diffraction as well as the variables which are used.

The diffracted field is equal to the Fresnel transformation of the distribution of amplitude on the abject surface. In the observation plane, this wave could equally be notated by the following simple equation :

Where is the complex amplitude modulus and is the phase. Given that the object is a natural diffusant, because it does not have a polished or light-reflecting surface, the diffracted field at the distance dimension is a speckle pattern. That is to say that the distribution of amplitude and phase in the observation plane is unpredictable. The phase is therefore unpredictable because of the coarse nature of the object's surface and we can observe that it is consistent around .

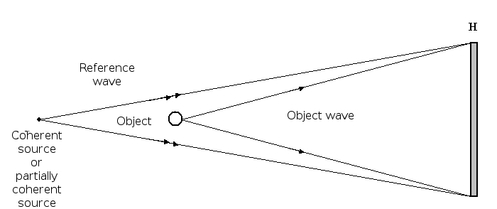
The process used in holography requires interferences to be formed in order to encode the information. Thus, the wave which is diffracted by the object is coherently mixed with a reference wave in the observation plane. The interferences between the two waves require the use of a temporally and spatially consistent source (typically a laser) and result in an intensity pattern which represents the modulus squared of the sum of the two complex amplitudes. Figure 2 illustrates the geometry of the interference scheme.

Thus, note that is the complex amplitude of the reference wave front in the recording plane :

Where is the modulus of the complex amplitude and is the phase of the wave front. The reference wave generally comes from a source pinhole : it is therefore spherically divergent and in oblique incidence on the recording material. If we take the coordinates of the source point as in the set of reference coordinates of the holographic plane , the optic phase of the reference wave is written in Fresnel's approximations as follows :

Its optic phase could also be written in the form :

Where are the information carrying spatial frequencies, is the radius of the curvature of the wave and is a constant. Generally, it turns out that the wave is uniform, that is to say that . The total illumination received by the holographic materials is written :

This equation could also be written under the form :

Thus represents the illumination of the holographic material at the time of the exposure. The received energy is a function of the exposure time and the illumination time so that :

The principal physical factors which characterise a photosensitive plate are the transmission factor where is the incident flux and is the flux transmitted by the recording plate after its processing, the optical density of the negative, , the saturation of the plate (W/cm2) and the average sensitivity of the latter (J/cm2).

The characteristic curve which connects the amplitude transmission with the photosensitive plate gives a linear zone centred on the exposure . The principal specificity of this plate is based on the following fact : if we take a sinusoidal exposure of the type in the recording linearity zone, then the amplitude transmission of the negative will be proportionate to the received illumination and we would get , as we can see in figure 3. The coefficient represents the derivative of the transmittance against the exposure at the coordinates for the average exposure.

Once the recording has been completed, the photosensitive plate is generally developed in a chemical bath in order to obtain a negative which encodes the phase and the amplitude of the wave from the studied object. In the linearity zone, the complex amplitude transmission of the negative is combined with the energy received by the photosensitive plate as per the following equation :

The average amplitude transmittance for this average exposure is annotated . The value of shouldn't go too far away from the operating point in order to stay within the linear transmission zone, which means that the sinusoidal fringes needs to be slightly adjusted. represents the average value of the exposure and is written as :

Thus we get : with .

Transmission holography is the most widespread type. During the recording of the hologram the wave diffracted by the object and the reference wave are recombined on the same side of the photosensitive plate.

There are two possible recording configurations: the “off axis” configuration and the “in line” configuration.

The “in line” configuration was the first to be used by Gabor. The reference beam and the object beam come from the same direction, illuminating the same side of the photosensitive plate. The studied object is placed between the light source and the photosensitive plate. This configuration doesn't require a particularly coherent light source.

It has only been possible to use the “off axis” configuration since the invention of lasers because this configuration requires the use of a highly coherent light source. The object beam and the reference beam are mixed together. The off axis recording system is represented by figure 5.

The light source must, in this case, be highly spatially and temporally coherent apart from when a perfect equilibrium can be assured between the abject and reference optical paths. Lasers fit these requirements. The coherence length is the determining parameter : this characteristic defines the acceptable difference between optical paths so that there is interference between the two waves.

During the recording of the hologram, the two waves both illuminate a different side of the photosensitive plate. The reference wave and the object wave are propagated in opposite directions and cause interference on the interference plane (figure 6).

Another technique consists of using a single laser beam which serves as both the object beam and the reference beam (figure 7). This method was proposed by Y.Denisyuk [ ]. The reference beam directly illuminates the holographic plate and illuminates the object, which is situated behind the plate, at short range. The wave, thus diffracted by the object, interferes with the reference wave at the level of the photographic plate (with emulsion on the object side). This system has the advantages of using just one laser beam, which makes it easier to carry out. The object field can thus be viewed in white light.

However, even though the quality of the reconstruction is realistic, the limited depth of the holographic field remains a major inconvenience. As with all reflection holograms, Denisyuk's holograms need to be “blanched”, that is to say transformed in to a phase hologram, before being fixed, so that their image can have sufficient clarity and luminosity.

In order to obtain a reasonable recording of the hologram, it is necessary for the material to be sensitive to the wave length of the monochromatic light source which is used. The response to the illumination of the plate should show a good linearity. “Analogue” plates offer very good resolutions, generally higher than (< )

Recorded holograms are divided into two categories :

• Amplitude holograms are made up of an interference pattern which results in a variation of either the transmission coefficient or the reflection coefficient in the recording plane; thus the amplitude of the reference beam is modulated by the hologram.

• Phase holograms encode the information using a variation in the refraction index or in the thickness of the photosensitive plate, which causes a modulation of the phase of the reference beam during reconstruction.

Table 1 sums up the principal materials which are used as photosensitive plates, the characteristics of these materials and the process of developing the negatives [ , ].

Silver halide photographic emulsions are the most used as recording materials; they have the advantage of being highly sensitive as well as presenting excellent spatial resolution. This type of plate allows the recording of both amplitude and phase holograms if a bleaching of the plate is carried out.

Bi-chromate gelatine allows for the production of phase holograms by photochemical reaction. The gelatine hardens depending on the level of illumination it is subjected to. The plate is simply washed with warm water in order to extract the gelatine which has not been exposed to the radiation. This material offers the best spatial resolutions.

Photo-resistant plates are organic photosensitive films. After the exposition and development stages, they produce phase holograms by variation of their thickness. They are rarely used because of their low sensitivity and because of the non-linear effects which are the product of low refractive efficiency.

Photopolymers are organic components which have the advantage of not needing to be treated by chemical solutions after exposure, thanks to photo-polymerisation. The information is encoded by variation of the thickness and the refraction index of the coating.

Photo-chromic plates have the considerable advantage of being reusable and don't require any preparation in the development stage. However, the given resolution is low compared to the silver photo plates. Because of their low sensitivity a high exposure time is required.

Photo-thermoplastic plates offer a certain ease of use given that they are reusable and can be developed on site, quickly and without chemical treatment. This type of plate used to be widely used in holographic interferometry [] it has almost fallen out of use nowadays, which has spurred on the development of digital holography.

Photorefractive crystals allow for the recording of a great number of phase holograms by photorefractive effect. They are often used in real-time in holographic interferometric applications []. The spectral sensitivity of these crystals is relatively narrow. However, these solutions have been the object of commercialisation ; thus, the company Optrion [] proposes a holographic camera which uses a BSO crystal as the recording plate. This camera is designed for photomechanical devices.