
Introduction
Light is composed of electromagnetic waves of which the propagation can be perfectly treated in accordance to Maxwell's equations. This is essential when optical elements modifying the propagation of luminous energy have very small dimensions, either close or inferior to the wavelength. Of course, it is not the case with the greatest majority of usual optical systems where one can consider the wave length to be infinitely small in comparison to their geometric dimensions.
The case is that which is concerned with the approximation of geometric optics where the undulatory nature of light is neglected, the interference, diffraction and polarization phenomena ignored. We demonstrate that the fundamental laws of geometric optics can be deducted from Maxwell's equations by shifting the wavelength towards 0.
Fermat's principle
Enunciated by Pierre Fermat in 1657, Fermat's principle acts as a foundation to geometrical optics. The main propagation laws are derived from it. The terms by themselves cannot be any simpler : light follows the shortest path in time. In fact, it can be demonstrated that it is the longest in somes cases, but in any case the path is extremal.
Geometrical optics suppose that mediums are isotropic. A medium is isotropic when the index is independent from the propagation direction and from the direction of light polarization. The index (xyz) is therefore perfectly defined on every point in space. If v(xyz) is the local propagation speed in medium and c the propagation speed in the void, we have in every way : n=c/v.
Propagation speed depends only on the point considered, it is independent from the direction of propagation.
Let us calculate propagation time TAB between two points in space A and B for a path effectively followed by light :
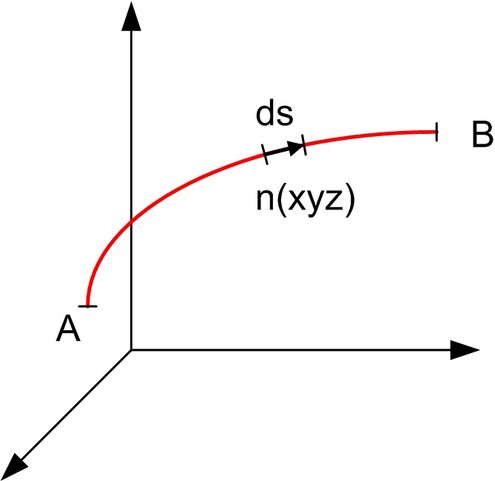
For a trajectory element of which the length is ds, propagation time dT is :
Total propagation time is therefore :
The path followed by rays of light is such that T is minimum or maximum.