Threshold Gain and Authorized Longitudinal Modes

A laser diode can be imitated by an active environment of length L defined by interfaces 1 and 2, which form the Fabry-Pérot cavity.

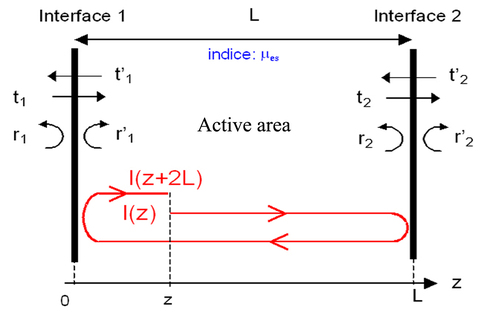
These interfaces are characterized by their reflection coefficients r and r' and their transmission coefficients t and t' in amplitude of the electric pathway. We will note as the effective sign of phase refraction without retro-injection.

The optical intensity flux I(z) follows an exponential law in où  is the absorption coefficient of the active environment, g is the gain of this environment and   is the loss coefficient owed principally to the absorption by free carriers (i.e. the Auger effect.)

The condition of laser emission is obtained as soon as the electric pathway associated with this flux is stabilized in its amplitude and phase by a return-trip to the active cavity where :

Where  is the threshold gain without feedback is the emission frequency without feedback, and c is the velocity of the light in the void.

The resolution of this equation in module and phase brings us to the threshold gain and to the frequency of authorized emissions.

A distinct authorized frequency corresponds to each value for u which is therefore a distinct longitudinal mode of possible laser emission. Careful, this study predicts nothing of the optical energy associated with each of these modes, which are theoretically infinite in number (numerous laser diodes are monomode).