Some usual examples of radiations

When the interface between two media is being illuminated, interaction between the photons and matter gives rise to three phenomena : reflection, transmission and absorption (figure 8), that depend essentially upon the following parameters of incoming light : angle of incidence, wavelength and polarization. Considering the input light is incident from a direction (θ',φ') and at a wavelength 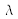, the interface is specified by the following spectral and directional properties :

• reflectance, R(λ,θ',φ'), or the percentage of incident light being sent back into the initial medium (at the same wavelength),

• transmittance, T(λ,θ',φ'),or the percentage of incident light going through the interface at the same wavelength,

• absorptance, A(λ,θ',φ'), or percentage of incident light being « digested » by the interface and then, as will be seen further down, converted into a spectrally wide radiation, called thermal radiation that depends upon the temperature of the interface.

In most applications, however, it is necessary to know the angular distribution of the light that is being reflected by the surface of an object when it is illuminated, for instance by the sensor itself. That kind of information is not available from the spectral and directional reflectance of the surface, defined above. To be convinved of that it is easy to realize that a wall and a polished mirror may have identical spectral reflectance, but will behave quite differently under some collimated and monochromatic illumination, because the first one (wall) is a diffuse surface and the second (mirror) a specular one.

The adequate parameter to use in order to specify the angular distribution of the reflected light from an interface under any kind of illumination is its spectral « Bidirectional Reflectance Distribution Function » or BRDF (λ,θ,φ,θ',φ') : BRDF (or BTDF for transmitted light) is the ratio between the radiance LR (λ,θ,φ) of the reflected (or transmitted) radiation towards a direction (θ,φ) and its irradiance E (λ,θ',φ'), when the surface is being illuminated at wavelength λ, and from a direction (θ',φ') :

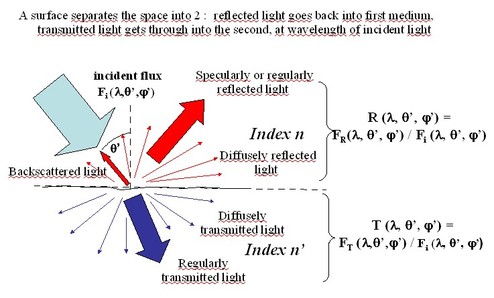
The angular diagram of the light that is reflected from a surface under collimated illumination varies from a surface to another. For that reason, surfaces are classified into different families, the two extremes being diffuse and specular (similar to mirrors) : a perfectly diffuse surface (also called lambertian surface) is such that the radiance of reflected light is constant : for a given direction of illumination, its BRDF is constant and equal to   times the value of its reflectance for that incidence angle.

The surfaces of most natural objects are diffuse, except for example those of calm waters (ponds, lakes). Optical diffuseness of a surface is strongly tied to its optical roughness, i.e. the fluctuations of its relief with respect to the incident wavelength. The angular behavior of light reflected by a diffuse surface usually depends upon the angle of incidence and wavelength: Most surfaces tend to become less and less diffuse (hence, more and more specular) with increasing wavelength and incidence angle, i.e. when one goes from the UV to visible, IR and radar), and from normal to grazing incidence. The behavior of specular surfaces will be examined later on along with that of optical surfaces.

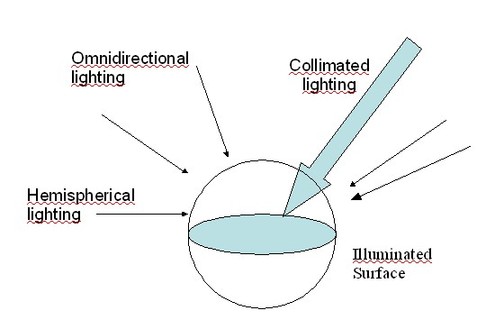
If one must design an electro-optical sensor that is intended to observe objects under some kind of (natural or artifical) illumination, one must know the exact conditions of illumination (figure 9), since the surfaces of objects react differently with respect to wavelength and to incidence angle. Hence, for a given value of irradiance, a given surface will appear quite differently if it is illuminated from a single direction (collimated lighting, for example by means of a laser, a flashlight, or the sun), from a set of different directions, or from all the directions inside the half-sphere seen by the surface (which is the case, in the visible, for a horizontal surface under blue sky).

At temperatures different from 0, any kind of body emits thermal radiation, due to the agitation of its electrons. Kirchhoff's law, below, shows that the spectral radiance of thermal radiation from a surface or a body X at temperature T, towards some direction (θ,φ) in space depends upon its spectral absorptance (introduced in the previous paragraph) for that direction and on its temperature :

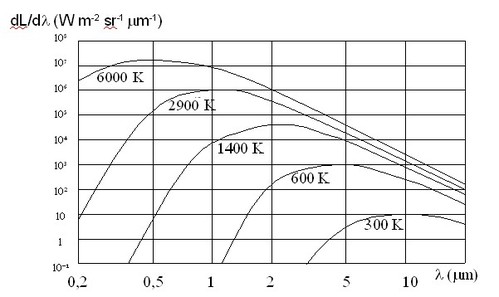
Since thermal radiation of a source is proportional to its spectral absorptance, this parameter has been in the past, and still is, called spectral directional emissivity ε(λ,θ,φ). of the material. The second term which appears on the right hand side of the above equation is the spectral radiance that the material λ and direction of incidence (θ,φ). The perfect absorber, or blackbody, has been the subject of numerous studies and played a fundamental role in the discovery of quantum mechanics. It can be shown that blackbody radiation is lambertian and unpolarized : its spectral radiance is uniform, and its value given (figure 10) by the following relationship (Planck's law) :

where h is Planck's constant ( h = 6,62 10-34 Js ),

c the speed of light in vacuum ( c≈ 3 108 ms-1 )

and kB Boltzmann's constant ( kB = 1,38 10-23 JK-1 )

In general, the total radiation from an object originates from reflection of ambient light and from thermal radiation. If some surface element, of temperature T, is receiving some spectral irradiance dE/dλ from direction (θ',φ'), its spectral radiance toward any direction (θ,φ) is :

If the surface is diffuse, and the illumination hemispherical (that is the case for numerous natural scenes), any source of light that is situated in the half-sphere in front of it will contribute to its radiance towards any direction inside a half-space, by means of the BRDF of the surface. On the contrary, if the surface is strictly specular, each direction of illumination will contribute by reflection only towards its symetric with respect to the normal, as ruled by the law of reflection, other directions of illumination being reflected elsewhere.

In case of natural scenes at ambient temperatures, the main origin of radiation strongly depends upon the spectral bandwidth of the observing sensor :

• In the visible and in the very near infrared, reflection of ambient light is the main contribution, because in that spectral domain, the spectral irradiance of the scene, due to the sun, is quite important and because reflectances of most objects are quite high, while BB thermal radiation at room temperature is infinitesimal.

• In the long wave infrared band (8-12 µm), thermal spectral radiance is at its maximum, while spectral irradiance from the sun is rather weak, as well as the reflectance of a vast majority of objects (most objects behave almost like blackbodies in that spectral band, except polished metals).

• In the midwave infrared band (3-5 µm), radiation from natural objects originates from both thermal emission and from reflection of ambient light during daytime and from thermal emission at night.