
Problem : Laser sensor for illumination and ranging of the moon
Capteur laser pour éclairage et télémétrie de la lune
Installed in several countries, a few pulsed laser systems illuminate a small area of the moon for precise ranging of the moon. We will consider that, for each pulse, the laser beam, of wavelength λ(= 1, 5 µm) radiate a peak power Pc (= 1 GW), during pulse duration τ(= 0,1 ns), with a total divergence
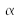 (= 10 µrad) and that its intensity is constant inside the cone (and naught outside). The ground of the moon, supposed to be perpendicular to the laser beam, is lambertian, and its diffuse reflectance at the laser wavelength is R ( = 0,1).
(= 10 µrad) and that its intensity is constant inside the cone (and naught outside). The ground of the moon, supposed to be perpendicular to the laser beam, is lambertian, and its diffuse reflectance at the laser wavelength is R ( = 0,1).
A telescope, situated near the laser transmitter, is aligned onto the laser impact on the moon. Its entrance pupil diameter is De (= 1m) and its aperture number is N (= 5)
Question
1) What is the number N0 of photons being emitted inside each pulse ?
Question
2) What is the peak laser radiant irradiance of the lunar surface ?
Question
3) What is the peak radiance Lp,moon and what is the peak intensity Lp,moon of the lunar area being illuminated by the laser, back towards the earth ?
Question
4) What is the number N1 of laser photons laser returning from the moon onto the detector of the telescope, if the detector diameter is Dd (= 100 µm) ?
Question
5) What would this number be, N2, if the existing detector was replaced by another one, smaller and of diameter D'd (= 60µm) ?
Question
6) In order for the photons to originate from a precisely known and small area of the moon, the laser beam is aligned onto a lunar region where a set of large cube corners (or retro-reflectors) have been deposited. Their collecting area is SRR (= 1m2) and their BRDF (= 107 sr-1). What is then the number of photons returning from the cube corners onto the detector at each of the laser echoes?