
Color systems RGB and CIE XYZ
A vector space for colors
Because of the trichromatic nature of vision, a color can be perfectly defined by a set of only three numbers, which can be thought of as the coordinates of a vector in a 3-D vector space. More precisely, a color can be represented by a vector whose magnitude is proportional to the light level (value) and whose orientation in space is related to the color tone itself (see figure 10).

In the example given in figure 10, a color
 is defined by a vector whose coordinates
is defined by a vector whose coordinates
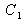 ,
,
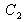 and
and
 (called trichromatic coordinates) are measured according to the basis vectors
(called trichromatic coordinates) are measured according to the basis vectors
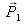 ,
,
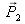 and
and
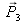 the “primary colors”. If the primary colors are non-metameric with respect to each other, they form a true basis for the vector space and one can write (1) :
the “primary colors”. If the primary colors are non-metameric with respect to each other, they form a true basis for the vector space and one can write (1) :
Equation (1) means that one can match the color
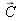 (i.e. find a metameric color of
(i.e. find a metameric color of
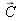 ) by a mixture of the three primary colors
) by a mixture of the three primary colors
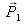 ,
,
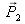 and
and
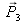 with the respective weights
with the respective weights
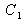 ,
,
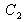 and
and
 .
.
Besides, one can think of any light spectrum
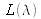 as being the result of an additive mixture of a large number of nearly-monochromatic light beams, adding up with a weighting function
as being the result of an additive mixture of a large number of nearly-monochromatic light beams, adding up with a weighting function
 which represents the spectrum, sampled with the delta function
which represents the spectrum, sampled with the delta function
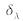 , so that :
, so that :
If
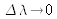 , we see that one can reproduce any polychromatic color
, we see that one can reproduce any polychromatic color
 by the following linear combination:
by the following linear combination:
where
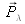 is a monochromatic primary color source of wavelength
is a monochromatic primary color source of wavelength
 . Any monochromatic source
. Any monochromatic source
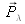 can be expressed in turn as a combination of three non-monochromatic primaries
can be expressed in turn as a combination of three non-monochromatic primaries
 ,
,
 and
and
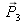 according to (1) which leads to :
according to (1) which leads to :
where
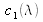 ,
,
 and
and
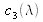 are the spectral tristimulus values which are determined once for all by the CIE from a set of human observers (see below). From (3) and (4) one gets:
are the spectral tristimulus values which are determined once for all by the CIE from a set of human observers (see below). From (3) and (4) one gets:
From (1), one gets the components
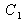 ,
,
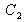 and
and
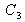 :
:
Once the spectral tristimulus values
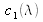 ,
,
 and
and
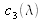 are known, any colored stimulus with a spectrum
are known, any colored stimulus with a spectrum
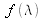 can be represented by a dot in a 3D space with coordinates
can be represented by a dot in a 3D space with coordinates
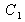 ,
,
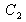 and
and
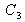 .
.
Measurement of spectral tristimulus values
An estimate of
 ,
,
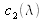 and
and
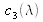 was performed in 1926 by J. Guild [] with 7 people with a limited visual field of 2°, so that the light was only incident on the central part of the retina, the macula (refer to the section “Basic mechanisms of color vision”). Primary colors were chosen to be monochromatic, at 700nm for red (
was performed in 1926 by J. Guild [] with 7 people with a limited visual field of 2°, so that the light was only incident on the central part of the retina, the macula (refer to the section “Basic mechanisms of color vision”). Primary colors were chosen to be monochromatic, at 700nm for red (
 ),546,1nm for green (
),546,1nm for green (
 ) and 435,8nm for blue (
) and 435,8nm for blue (
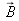 ). The observation field was divided into two sections (see figure 11), one of them was illuminated by a monochromatic source, while the other received a combination of the three primary sources, which superimposed by additive mixing on the eye of the observer. The observer could tune the light level of the primary sources (by changing the position of the sources or by directly varying the intensity through calibrated apertures) until matching of visual perceptions was reached.
). The observation field was divided into two sections (see figure 11), one of them was illuminated by a monochromatic source, while the other received a combination of the three primary sources, which superimposed by additive mixing on the eye of the observer. The observer could tune the light level of the primary sources (by changing the position of the sources or by directly varying the intensity through calibrated apertures) until matching of visual perceptions was reached.

When the “test source” to be matched for this experiment is a monochromatic source of wavelength
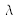 he trichromatic components obtained are called the RGB tristimulus values
he trichromatic components obtained are called the RGB tristimulus values
 ,
,
 and
and
 . They were tabulated in 1931, so that this system is sometimes called RGB CIE 1931 system. They are plotted versus wavelength in figure 12.
. They were tabulated in 1931, so that this system is sometimes called RGB CIE 1931 system. They are plotted versus wavelength in figure 12.

The Y scale is defined so that
 .
.
This choice is justified by the fact that the visual perception of a neutral stimulus (white or gray color) corresponds to a balanced response of the three different cones. It has to be noticed that for wavelengths below 550nm, the color functions
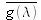 and
and
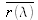 take negative values. This is because it is impossible to match a monochromatic color below 550 nm by adding three monochromatic primaries. Therefore, in the setup shown in figure 11, matching of color perceptions in the two halves of the observation field would be obtained for some colors if one adds some light from one of the primaries to the “test light”.
take negative values. This is because it is impossible to match a monochromatic color below 550 nm by adding three monochromatic primaries. Therefore, in the setup shown in figure 11, matching of color perceptions in the two halves of the observation field would be obtained for some colors if one adds some light from one of the primaries to the “test light”.
Graphical representation – Color triangle
From (5), any polychromatic radiation with a luminance
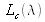 is associated with a color
is associated with a color
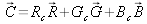 where the trichromatic coordinates in the RGB color system are given by :
where the trichromatic coordinates in the RGB color system are given by :
Since only the relative values of these coordinates have a physical meaning in terms of chromaticity, it is usual to introduce the trichromatic coordinates
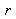 ,
,
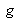 and
and
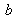 given by:
given by:
In practice, it is easier to represent colors in a plane rather than in the 3-D space. We have, from (7):
which is the equation of a plane defined by the 3 terminal points of the unit vectors
 ,
,
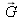 and
and
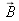 (see figure 13).
(see figure 13).

A color
 is then represented by a point (
is then represented by a point (
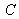 ) in that plane. Since the component
) in that plane. Since the component
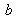 can be straightforwardly derived from (8) provided that
can be straightforwardly derived from (8) provided that
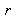 and
and
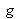 are known, one generally prefers to display the plane
are known, one generally prefers to display the plane
 under the form of a right isosceles triangle in which
under the form of a right isosceles triangle in which
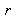 and
and
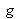 lie along the right axes of the triangle.The diagram obtained is called the (r, g) chromaticity diagram, displayed in figure 14. Monochromatic radiations (for
lie along the right axes of the triangle.The diagram obtained is called the (r, g) chromaticity diagram, displayed in figure 14. Monochromatic radiations (for
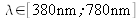 ) lie along the so-called spectrum locus. They correspond to the following coordinates (with
) lie along the so-called spectrum locus. They correspond to the following coordinates (with
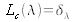 ) :
) :
At the three corners of the triangle appear the (monochromatic) primary colors red (
 ;
;
 =700nm), green (
=700nm), green (
 ;
;
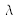 =546,1nm) and blue (
=546,1nm) and blue (
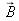 ;
;
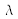 =435,8nm). The line connecting the red and blue primaries is called the purple line.
=435,8nm). The line connecting the red and blue primaries is called the purple line.

All existing colors have their associated points inside the domain delimited by the spectrum locus and the purple line. Points outside of this area have no physical meaning and do not correspond to real stimuli.
XYZ color space
As it can be seen on figure 14, many colors have negative trichromatic coordinates in the RGB system, as a result of the choice of three monochromatic primary colors. In order to eliminate this drawback, a linear transformation over the RBG space is made, leading to the tristimulus values
 ,
,
 and
and
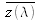 which take only positive values. Moreover, the primaries
which take only positive values. Moreover, the primaries
 ,
,
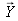 and
and
 (no longer monochromatic) have been chosen in such a way that the plane
(no longer monochromatic) have been chosen in such a way that the plane
 corresponds to a zero-luminance plane, and that the axis
corresponds to a zero-luminance plane, and that the axis
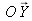 becomes the axis of visual luminances. Indeed, for a stimulus having a luminance
becomes the axis of visual luminances. Indeed, for a stimulus having a luminance
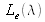 in energetic units, we know that the luminance in visual units
in energetic units, we know that the luminance in visual units
 is :
is :
With
 (in photopic vision), where
(in photopic vision), where
 is the luminous efficiency function (refer to a basic photometry course to learn more about
is the luminous efficiency function (refer to a basic photometry course to learn more about
 ).Using our usual trichromatic notations, we see that if we define the Y coordinate as
).Using our usual trichromatic notations, we see that if we define the Y coordinate as
 then
then
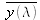 is identical to
is identical to
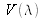 , so that one of the trichromatic coordinates will give directly the visual luminance.
, so that one of the trichromatic coordinates will give directly the visual luminance.
The linear transformation
 is defined by [] :
is defined by [] :
which gives the tristimulus values vs. wavelength shown in figure 15.

A color is represented by a vector whose trichromatic coordinates
 ,
,
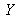 ,
,
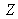 are :
are :
from which one can define the trichromatic coordinates
 ,
,
 ,
,
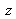 such as :
such as :
Since
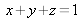 , colors are represented in a plane
, colors are represented in a plane
 whose axes x and y form right angles. Monochromatic colors (
whose axes x and y form right angles. Monochromatic colors (
 )which have coordinates given by
)which have coordinates given by
lie along the spectrum locus. As for the RGB system, the surface inside which one may find all real physical colors is delimited by the spectrum locus and by the purple line. This surface is embedded within a circumscribing triangle whose corners
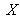 ,
,
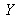 ,
,
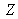 represent the three primaries :
represent the three primaries :
-
the primary
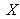 :
:
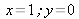
-
the primary
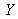 :
:

-
the primary
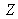 :
:

These primaries are non real since they are outside of the chromatic gamut (cf. figure 16).

Figure 17 shows the chromaticity diagram xy CIE 1931 with the corresponding color names for an observer in daylight conditions []. The central zone around the position of white (equienergetic stimulus) corresponds to the CIE normalized illuminants.

Equienergetic stimulus
By definition, the spectrum of an “equienergetic stimulus”
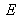 (perfect white) is constant over the whole visible spectrum, that is
(perfect white) is constant over the whole visible spectrum, that is
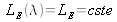 , or
, or
and
since
This is valid in the RGB system, but it remains true in the
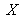 ,
,
 ,
,
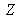 color system, in which we may write
color system, in which we may write
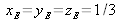 . The representative point of stimulus
. The representative point of stimulus
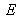 is located at the center of the RGB or XYZ triangle (see figures 14 and 16).
is located at the center of the RGB or XYZ triangle (see figures 14 and 16).
Dominant color – complementary color
Within the
 diagram, a color
diagram, a color
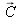 resulting from the additive mixing of two colors
resulting from the additive mixing of two colors
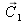 and
and
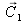 such as
such as
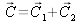 will result in three representative points
will result in three representative points
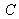 ,
,
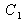 and
and
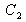 aligned along the same line (see figure 18).
aligned along the same line (see figure 18).

In a similar fashion, any color
 can be thought of as an additive mixing of the white equienergetic stimulus
can be thought of as an additive mixing of the white equienergetic stimulus
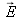 with a pure color lying along the spectrum locus. The latter is called the dominant color
with a pure color lying along the spectrum locus. The latter is called the dominant color
 with
with
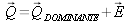 .
.
Conversely, the white equienergetic stimulus
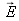 could theoretically be obtained upon additive mixing of any color
could theoretically be obtained upon additive mixing of any color
 with a pure color called the complementary color
with a pure color called the complementary color
 such as
such as
 .
.
The ratio
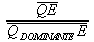 is a measure of the purity of the color
is a measure of the purity of the color
 . This ratio is equal to 0 for the equienergetic white and is equal to 1 for a pure monochromatic color.
. This ratio is equal to 0 for the equienergetic white and is equal to 1 for a pure monochromatic color.