Optical metrology through fractional Fourier transforms

Linear frequency

We want here to point out the usefulness of fractional Fourier transforms to analyse linear frequency chirped signals also called chirps. These signals are characterized by the linear evolution of their spectral contents. The harmonic signal is defined by:

(1.1)

And its instant frequency is:

(1.2)

Where is the phase of   . The signal   is said to be stationary if for any the instantaneous frequency  is constant [Fla98]. The standard Fourier transform is well adapted to analyse such signals. The FT of  allows us to point out its spectral properties synthetically. This function is a Dirac impulsion centred on the  frequency.

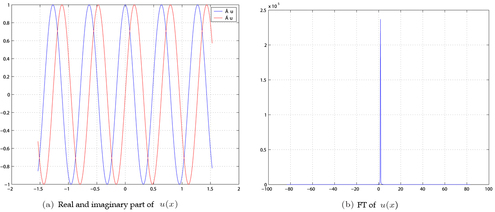
Figure 1
Figure 1 [zoom...]Info

* Figure 1: Representation of 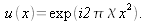(1.3) and its FT.

Figures 1(a) and (b) represent   and its FT. If the function   is the linear frequency chirped function so that:

(1.3)

Its fractional Fourier transform is equal to:

(1.4)
(1.4) [zoom...]

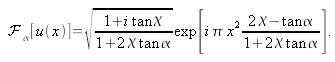
For  we find the standard Fourier transform which is again a chirped function. Conversely, for   and when using equality [H.01]:

(1.5)

We obtain:

(1.6)

This time the Dirac distribution is centred on the origin of the coordinates. The function ) is therefore a centred function.

The fractional order defines the frequency drift. Fractional Fourier transforms allow us to detect linear chirps in a signal.

Figure 2
Figure 2 [zoom...]Info

* Figure 2: Representation of and its optimal order FFT.

Figures 2(a) and 2(b) illustrate this property. Besides, this property will allow us to conduct a metrology since diffraction phenomena in Fresnel's approximation have a linear frequency drift.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)The detection of linear frequency chirped functionsPropagation in a clear space and fractional Fourier transforms