Optical devices tunable strains

Tunable gratings like GLV or polychromators can be considered digital systems as the actuation is the result of a change in the grating period and its profile modulation in tiny quantities, with the same size as micro machined tapes. Since then, the “reconfigurability” is limited by the smallest dimension allowed by the lithography process. To open very small scale possibilities, it was necessary to implement a new range of “analogical” tunable grating. Nanopositioning was an additional functional possibility given by these devices, necessary to allow a rather precise reset for optical applications. But another aspect is sacrificed as these analogical devices are not appropriate, for instance, to have polychromators functions in a correlation spectrometry.

Diffraction grating analogical scanning is get by a transverse activation of the grating structure by using a piezoelectric thin film actuator or interdigitated electrodes with folded up grating, as in the picture below.

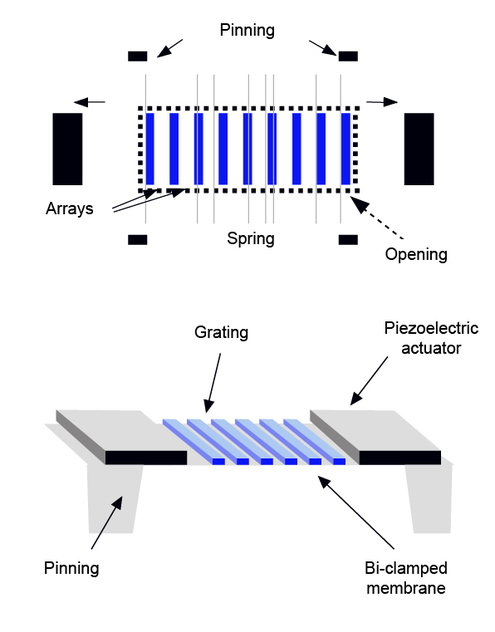
To get the transverse actuation, the grating etchings are made on a deformable membrane in suspension. The membrane is mechanically tightened by thin film piezoelectric actuators made of a lead zirconate titanate between two superior and inferior electrodes, located at the ends of the membrane. These piezoelectric actuators can produce a power strong enough to stretch the membrane until a 0.3% constraint or until producing a 0.3% variation of the diffracted angle under the influence of an electric field across the piezoelectric film. The tenseness of the piezoelectric film leads to a mechanical constraint on the membrane in the transverse direction.

Considering the possibility of a very precise control of the voltage on a piezoelectric thin film, we can get a resolution better than 0.05nm in the period variations of the grating corresponding to an angular resolution better than 2.1µrad whereas the current possibilities of metrology do not permit an observable resolution inferior to the nanometer scale. Membrane rotations and torsions outside the balance plan, the asymmetrical rotations during the actuation, thermal disturbance, vibration and optical detection techniques can limit the thinnest available resolution. The display of tunable diffraction gratings allowed to see the accordability of the diffraction angle from the first order until 486µrad under 10 V with minimal movements observable from the grating period of approximately 0.6 under 1 V.

Reconfigurability combined with nanopositioning lead to interesting application possibilities for accordable grating devices.

The “optical diversity technique” is another interesting way that has been developed to balance the limitation of the grating spectrometers opening. In a few words, here is the problem: the spectral resolution of a grating spectrometer is determined by the number of N periods of the grating. So, as the available surface is (by definition) very small in a miniature spectrometer, the spectrum we get can be blurred. In other words, the measured value of the spectral density at one wavelength doesn't correspond to real value of the tested sample but it also has contributions from other neighboring wavelengths (this is call the convolution phenomena). Of course we can go back the real spectral density thanks to a deconvolution operation, knowing the impulsional response of the grating which depends on N and the impulsional response of the light collection optics.  This deconvolution can be made digitally with a post-treatment of the measured spectrum. But the deconvolution operation is very sensitive to noise inherent in every measure. We found out that, by scanning the grating and repeating the spectral measure, we could get the blurred spectrum back with a much more weak sensitiveness to noise and, as a consequence, a so much better definition.

Optical diversity works that way: the grating period is first fixed to an initial value and a first blurred measured is taken. Then the grating is activated in such a way that the period is changing of a few quantities and a second blurred measure is taken. We repeat this process according to the noise we heard. The weaker the signal-to-noise ratio is, the greater the number of necessary measures is. Then the group of get spectra is treated by using a class of mathematical operation called “regularized pseudo-inverse method”. After this step, we get the final spectrum. The quality of the signal treatment process is linked to the measure noise level and to the grating actuation precision and definition. It emerges that optical diversity is a good example to show how reconfigurability and nanopositioning can help to solve an important optical problem due to spectrometers miniaturization.