Peuplement des "niveaux du bas" à température ambiante
Afin de connaître l'efficacité d'une transition laser, il est important de savoir si le niveau du bas est peuplé ou non à l'équilibre thermodynamique. Pour cela, on applique la loi de Boltzmann :
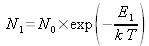, N0 étant la population du niveau fondamental dont l'énergie est prise à 0, N1 étant la population du niveau d'énergie E1 que l'on considère.
Afin d'en avoir une utilisation facile, on peut convertir l'énergie "thermique" kT en cm-1 grâce à la formule donnée en remarque ci-dessous. Pour une température de 300 K, on trouve kT=208 cm-1.
A partir de la relation entre une fréquence et un niveau d'énergie :
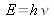, on peut en déduire la relation entre les énergies exprimées en nombre d'onde et les énergies exprimées en joule : E(J) = 100 h c E(cm-1)
En appliquant la loi de Boltzmann, on peut donc montrer que les niveaux du bas pour les transitions à 1064 nm et à 1320 nm ne sont pas peuplés car ils sont situés à plusieurs milliers de cm-1 du niveau fondamental : le rapport E1/kT est alors très faible.
En revanche, le niveau du bas (Z5) pour la transition à 946 nm a une énergie qui est du même ordre de grandeur que kT. 1,6 % de la population du niveau fondamental se trouve dans le niveau du bas. Pour réaliser une inversion de population, il faudra donc mettre au moins la même quantité d'ions dans le niveau du haut et cette quantité ne sera pas utilisable pour l'amplification par émission stimulée, d'où une perte d'efficacité par rapport aux transitions précédentes.