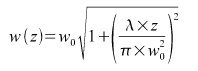Rappels sur les faisceaux Gaussiens

Le rayonnement issu d'un laser peut être considéré comme gaussien. Pourquoi considérer des ondes gaussiennes plutôt que sphériques ou planes? Car ces ondes simples obligent à considérer le phénomène de diffraction en raison de leur extension infinie dans les directions transverses à la propagation. Ce phénomène est alors incompatible avec l'effet laser d'où le faisceau gaussien.

Cette onde comme l'onde sphérique et l'onde plane est solution de l'équation d'onde. Elle a pour expression la formule suivante :

A(z) représente l'amplitude complexe du champ suivant z. Dans cette expression, les variations du champ E suivant la coordoonée radiale r sont contenues dans les termes en exponentiel.

• Le terme en 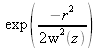justifie le caractère gaussien du faisceau. Pour une distance fixée z, l'amplitude du champ diminue d'un facteur 1/e2 à une distance r=w(z) de l'axe optique. Le rayon w(z) est donc une mesure de l'extension radiale du faisceau.

• De manière identique à l'onde sphérique paraxiale, le faisceau gaussien est ici caractérisé par des fronts d'ondes de rayon R(z).

Sur la figure précédente, pour z=0, on peut définir un rayon de ceinture ou col du faisceau ω0 qui représente la valeur minimale du rayon ω(z). Ce paramètre est primordial, puisqu'il permet d'exprimer les grandeurs caractéristiques suivantes :

La longueur de Rayleigh zR représente donc une mesure de la divergence du faisceau. En effet, plus cette grandeur sera petite, plus le faisceau sera divergent. Cette divergence, comme il est montré sur la figure précédente peut aussi se mesurer par le comportement asymptotique du rayon w(z). Lorsque z>>zR devient :

et la pente associée s'écrit par