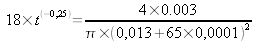SECTION C : Distance nominale de risque oculaire (DNRO)
Rappels : La DNRO représente la distance à laquelle l'éclairement énergétique ou l'exposition énergétique tombe en dessous des EMP appropriées.
L'éclairement énergétique à une distance z d'une source laser est donnée par la formule suivante :
En supposant que le profil du faisceau laser est gaussien, la lettre ω représentant le rayon du faisceau mesuré en 1/e en champ du faisceau et Φ est la divergence du faisceau. exp(-l.μ) est un facteur d'atténuation atmosphérique qui est souvent négligé. Cette formule est valable quelque-soit la position de l'observateur par rapport à la sortie du laser.
Pour évaluer la DNRO, on pose z=DNRO et E=EMP.
Dans ce cas, si on néglige l'influence de l'absorption de l'atmosphère, on obtient l'expression suivante :
Cette dernière expression est vraie si et seulement si le faisceau se propage librement dans l'espace. Si un instrument optique est utilisé pour observer une source de rayonnement laser, il faut majorer la DNRO pour tenir compte d'un niveau d'énergie beaucoup plus important dans l'oeil. Du fait de la collimation du rayonnment issu de la source par l'outil optique.
Cet accroissement du niveau de flux peut être pris en compte grâce au paramètre de majoration suivant :
Question
Exercice 3.1 : Soit un laser délivrant un rayonnement lumineux continu de longueur d'onde centrale 400nm. La puissance moyenne délivrée par ce laser est de 4W et la divergence naturelle du faisceau est de 0,7 mrad et le diamètre du faisceau en sortie de laser est de 1mm.
-
Dans un premier temps, donnez l'EMP appropriée en supposant que le temps d'exposition est de 2h.
-
Calculer ensuite la DNRO, sachant que le faisceau se propage dans l'air. En d'autres termes l'atténuation atmosphérique peut être négligée.
Question
Exercice 3.2 : Pour limiter la divergence naturelle du faisceau, on place un système optique afocal grossisseur permettant ainsi de collimater le faisceau et de dilater le diamètre du faisceau. Après optimisation de ce système, la divergence du faisceau n'est plus que de 0,1 mrad et la taille du faisceau est de 7mm. Calculez la nouvelle DNRO.
Question
Exercice 3.3 : Un laser de topographie He-Ne (632 nm) émet un rayonnement dont la puissance moyenne est de l'ordre de 3mW. Le faisceau issu de la cavité possède un diamètre initial de 13 mm et s'élargit au fur et à mesure de la propagation dans l'air. A 50 m de la source le faisceau atteint un diamètre de 18 mm.
-
Pendant combien de temps peut on observer directement le faisceau issu de la source sans danger lorsque notre oeil se situe à 65 m de la source?
-
Evaluez la distance minimale de vision directe sans danger de ce laser pour une durée d'exposition de l'ordre de 3min?
Question
Exercice 3.4 : Un télémètre à laser au verre dopé au néodyme déclenché émet un rayonnement impulsionnel de longueur d'onde 1060 nm. La puissance lumineuse est de 1,5 MW soit une énergie par impulsion égale à 45mJ. La fréquence de répétition du laser est de 12 impulsions par minute. Le diamètre du faisceau à la sortie du laser est de 10 mm et la divergence naturelle du faisceau est de 1 mrad.
-
Calculez la DNRO lorsqu'un oeil nu est sous exposition du rayonnement.
-
Calculez la DNRO, lorsque le faisceau est observé au travers d'une optique de 60 mm de diamètre.