
Stabilité d'une cavité
Étude générale
Considérons une cavité représentée par une structure périodique d'éléments optiques. La matrice de transfert de l'ensemble est
 (voir plus haut).
(voir plus haut).
Pour n périodes, soir n aller-retours dans le cas d'une cavité linéaire, la matrice de transfert est Tn. Si on note
 le vecteur représentant un rayon à l'entrée de la séquence, et
le vecteur représentant un rayon à l'entrée de la séquence, et
 le vecteur à la sortie, on a
le vecteur à la sortie, on a

La matrice T est diagonalisable, et si on note P la matrice de passage unitaire et x1,2 les deux valeurs propres de T, on a (voir un cours d'algèbre linéaire)
 .
.
On en déduit donc que
Pour que la cavité soit stable, il faut que les rayons restent au voisinage de l'axe optique au cours de la propagation à travers les n éléments quand n tend vers l'infini. Autrement dit, il faut que pn soit borné supérieurement, ou encore que
 et
et
 .
.
Par ailleurs, les valeurs propres x1 et x2 de T obéissent aux relations suivantes (voir cours d'algèbre linéaire):
Comme x1 est à priori un complexe, on pose
 et par suite
et par suite

Donc comme
 , on a forcement
, on a forcement
 . Ensuite, la relation faisant intervenir la trace de T conduit à
. Ensuite, la relation faisant intervenir la trace de T conduit à
 .
.
On en déduit la condition de stabilité applicable à toute cavité :
ou encore
Une cavité est stable quand les coefficients de sa matrice vérifient la condition de stabilité énoncée ci-dessus.
Exemple d'application
Prenons une cavité linéaire simple de longueur d à deux miroirs de rayons de courbures R1 et R2, équivalente à une séquence périodique de deux lentilles minces de focales f1 (=R1/2) et f2 (=R2/2), séparées d'une distance d.
La matrice T vaut (voir figure 4):
On montre alors facilement que
On a l'habitude de poser
 et on obtient la condition de stabilité de la cavité pour une cavité linéaire à deux miroirs :
et on obtient la condition de stabilité de la cavité pour une cavité linéaire à deux miroirs :
On visualise classiquement cette condition de stabilité sur un diagramme représentant l'espace g2(g1), c'est à dire en prenant g2 comme axe des ordonnées et g1 comme axe des abscisses (figure 7).
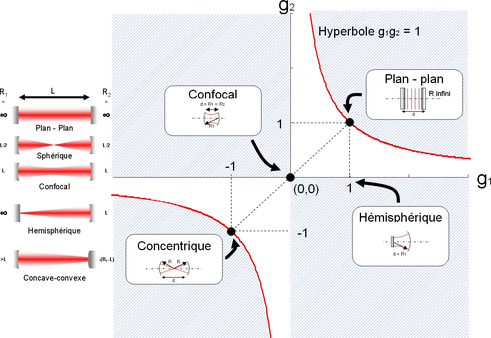
La condition de stabilité est alors représentée par deux hyperboles, et les zones d' instabilité sont hachurées sur la figure.
Quelques cas particuliers sont remarquables :
-
sur l'hyperbole g1g2=1 : on a alors d=R1+R2, ce sont les cavités dites concentriques.
-
Les droites g1=1 et g2=1 correspondent à des cavités où l'un des miroirs est plan (rayon de courbure infini). La cavité Fabry-Pérot (2 miroirs plans) est obtenue pour g1=g2=1.
-
Pour R1 = R2 =d (g1 = g2 = 0), on a une cavité dite « confocale ».
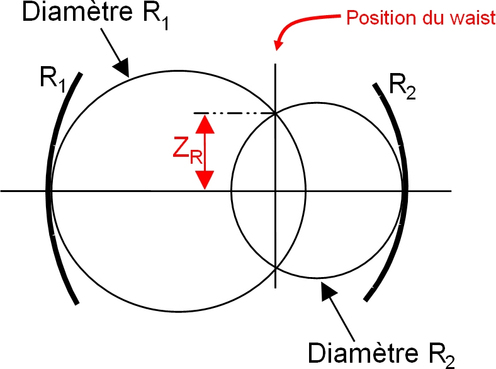
Il existe une méthode graphique, dite « méthode des cercles de Deschamps », qui permet de savoir si une cavité à deux miroirs sphériques est stable : il suffit de vérifier que les deux cercles de diamètres R1 et R2 centrés sur les points focaux F1 et F2 se coupent (voir figure 8). Si c'est le cas, la cavité est stable (on peut vérifier que cela est une conséquence directe de la formule établie plus haut).
Les cercles de Deschamps permettent également d'avoir accès (voir figure 8) à la position du « waist » (intersection des cercles) et à la « longueur de Rayleigh » ZR , deux paramètres qui seront définis dans la suite de ce cours.
Cavités instables
Il n'est pas obligatoire de disposer d'une cavité stable pour obtenir un effet laser. Dans certains cas, lorsque le gain du milieu laser est suffisant pour permettre des pertes très élevées, les résonateurs instables présentent des avantages importants. C'est en particulier le cas des lasers de très haute puissance.
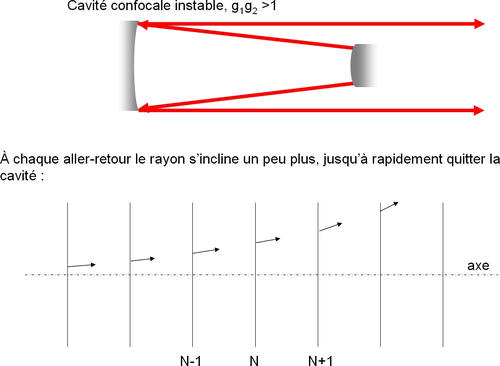
L'avantage principal de ces cavités est que le volume du mode dans la cavité peut être important, ce qui diminue la densité de puissance sur les miroirs (important pour les lasers de fortes puissances, où les seuils de dommage sont rapidement atteints). De plus, les modes transverses subissent de très fortes pertes, et ces cavités oscillent donc naturellement sur leur mode fondamental en général.
Ces cavités ne sont possibles qu'avec des milieux à très fort gain puisqu'un rayon donné ne fait que quelques passages dans le milieu amplificateur avant de s'échapper de la cavité.