Faisceau en sortie

A quoi va ressembler le faisceau à la sortie du laser, à travers le miroir sphérique ?

Ce miroir est partiellement transparent, et possède une face sphérique concave (c'est la face utile pour la cavité) et une face plane (l'arrière du substrat sur lequel est déposé le miroir).

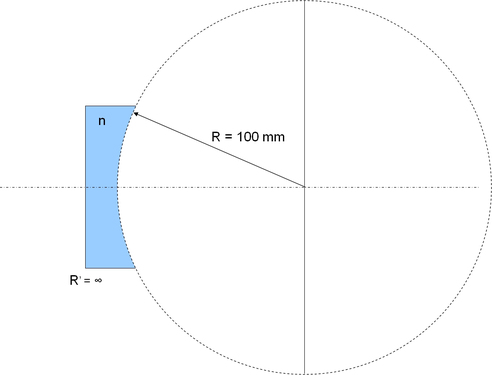
Le miroir de sortie se comporte donc vis-à vis du faisceau laser sortant comme une lentille divergente.

Sa focale f' est donnée par la « formule des opticiens » (voir cours d'optique géométrique) :

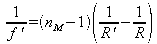avec R' = rayon de la face plane = infini et nM l'indice du substrat sur lequel est déposé le miroir.

On a donc 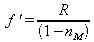, soit numériquement en prenant nM = 1,5 (verre) : f' = -200 mm.

On a déjà déterminé la divergence du faisceau dans la cavité. Combien vaut-elle maintenant en dehors ?

On va chercher le nouveau rayon de courbure complexe après le miroir de sortie, soit après une lentille divergente de focale f' . Pour cela, on applique la loi ABCD :

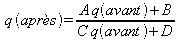en notant q(avant) le rayon de courbure complexe avant traversée du miroir de sortie et q(après) le rayon de courbure complexe après traversée de ce même miroir.

Les coefficients ABCD sont ceux de la matrice de transfert d'une lentille :

On en déduit que :

NB : c'est une formule utile dans bien des cas lorsque l'on transforme un faisceau gaussien via une lentille.

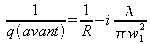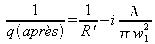On a également et (la taille du faisceau ne change pas entre les deux faces de la lentille dans l'hypothèse « lentille mince »).

On en déduit que par identification que .

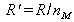En utilisant la formule du cours :

avec la nouvelle valeur de R', on trouve le « waist effectif » pour le faisceau sortant de la cavité :

En remplaçant w1 par sa valeur en fonction de w0 trouvée précédemment , soit 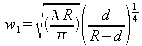on trouve :

Comme de plus 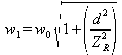et 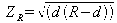on en déduit :

On en déduit la nouvelle divergence  :

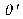Numériquement, la nouvelle divergence vaut 1,438 fois celle avant le passage par le miroir de sortie (on a pris ici les valeurs pour d=85,5 mm – voir figure 4) soit 4,3 mrad.