Diffraction de Fraunhofer d'un réseau d'amplitude sinusoïdal

Jusqu'à présent la transmittance t(x,y) de l'ouverture était définie de façon binaire ('0' à l'extérieur, '1' à l'intérieur). On peut introduire des distributions spatiales absorbantes (par exemple à l'aide d'un négatif photo) et obtenir ainsi toutes les valeurs de t comprises entre '0' et '1'.

Considérons un réseau d'amplitude sinusoïdal limité par une ouverture carré de côté L :

où f0 est la fréquence spatiale du réseau et m représente la variation crête à crête de l'amplitude. m est appelé profondeur de modulation de l'amplitude (voir figure EC1(a)).

Dans la figure EC1(b) on peut voir l'image de ce réseau. Evidemment le pas de ce réseau est agrandi volontairement dans cette figure pour visualiser la transmittance sinusoïdale.

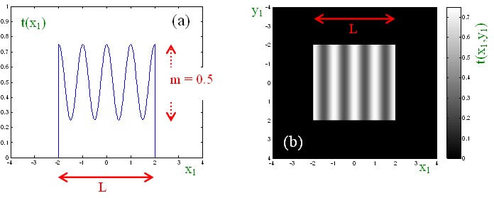
Si l'écran est éclairé sous incidence normale par une onde plane monochromatique d'amplitude unité, la distribution du champ dans l'ouverture est tout simplement égale à t(x1,y1).

La figure de diffraction de Fraunhofer passe par le calcul de la TF(t) :

Soient :

Par suite de la distributivité du produit de convolution :

Or pour translater une fonction f(x,y) il suffit de faire sa convolution avec la translatée de la distribution de Dirac (δ(x-a)) :

Donc

D'où la distribution du champ en amplitude :

Dans la figure EC2(a) sont représentées les 3 fonctions sinus cardinal centrées sur -f0, 0 et +f0 dans le cas où m=1.

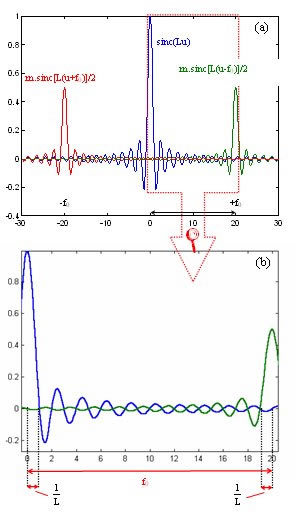
Un agrandissement de cette figure est visible dans la figure EC2(b) où on peut voir la largeur du lobe central des deux fonctions sinc centrées en 0 et +f0.

Si , le produit de ces deux fonctions peut être négligé car lorsque l'une est au maximum l'autre a des valeurs proches de zéros. On peut donc négliger le chevauchement entre les 3 fonctions sinc. Lorsqu'on calcule l'intensité, les produits croisés entre ces fonctions est négligeable devant le carré de chacune de ces fonctions.

En définitif, l'intensité dans le plan d'observation devient :

Dans la figure EC3(a) on peut voir l'image de la figure de diffraction obtenue à partir de l'équation précédente.

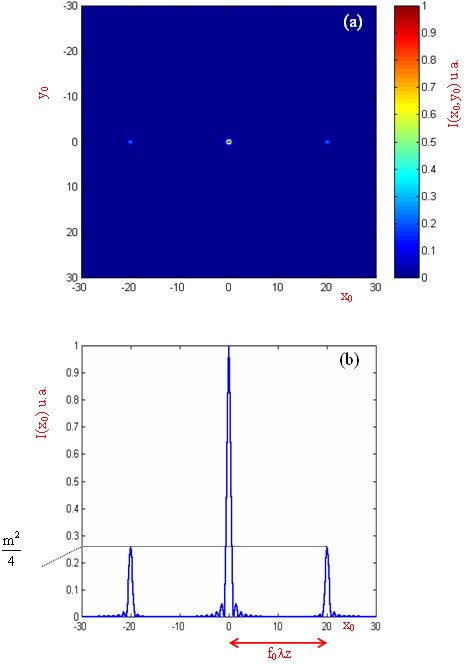
Une partie de l'énergie lumineuse est déviée suivant deux figures latérales. La partie centrale est appelée composante d'ordre zéro alors que les deux lobes latéraux sont appelés composantes du 1er ordre. Dans la figure EC3(b) on peut voir l'évolution de la répartition de l'intensité normalisée (pour y0 =0) lorsque m=1. Noter que la distance qui sépare les ordres de diffractions par rapport au centre est f0λz. Par ailleurs, dans le meilleur des cas, lorsque m=1, l'intensité des lobes diffractés ne peut dépasser 0,25 pour un réseau sinusoïdal en amplitude.