Formalisme de Maxwell

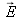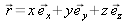Pour représenter une onde lumineuse, on lui associe comme grandeur physique les champs électrique et magnétique , décrits par une fonction de l'espace et du temps t. Maxwell a montré que ces deux champs se propagent de façon couplée dans un milieu selon les équations suivantes (connues sous le nom « d'équations de Maxwell ») [1] :

où  est la perméabilité du milieu, 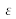 est la permittivité du milieu,  est lié aux charges libres et de polarisation du milieu et est lié aux courants de conduction et de polarisation du milieu. Pour le vide, 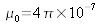et 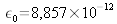et on a ,  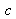étant la vitesse de propagation dans le vide . Dans un milieu linéaire, homogène et isotrope, en absence de charges libres, nous avons , et  est une constante. C'est le cas, par exemple, du verre non contraint ou de l'air.

Les équations de Maxwell conduisent aux équations de propagation des champs magnétiques et électriques dont la forme générale est :

où est l'opérateur Laplacien vectoriel (on a ), n est l'indice de réfraction du milieu de propagation. Cette équation est également vérifiée par le champ magnétique.

On remarque que toutes les composantes de , {Ex,Ey,Ez}, et de ,{ Bx,By,Bz}, suivent la même équation de propagation :

et ainsi pour {Ey, Ez, Bx, By, Bz}.

Il est donc possible de synthétiser le comportement de ces composantes, par une unique onde scalaire 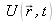régit par l'équation de propagation,

représentant l'une des composantes {Ex, Ey, Ez, Bx, By, Bz}.

Une onde polarisée rectiligne suivant x s'écrit :

avec :

Dans le cas où la propagation de l'onde présente une symétrie sphérique, le changement en coordonnées sphériques amène à l'équation d'onde suivante :

où .