Interféromètre à ondes multiples
Un dispositif simple peut être constitué par une lame de verre d'épaisseur
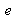 et d'indice
et d'indice
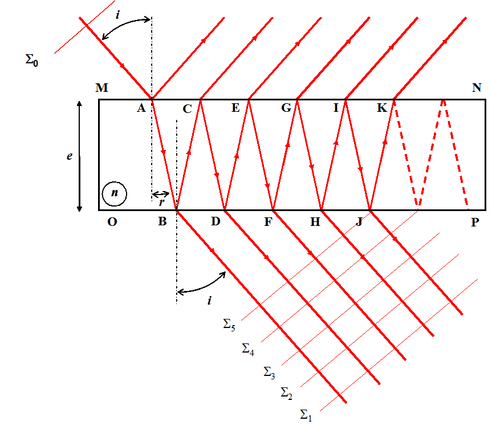
 éclairée par une source monochromatique à l'infini, c'est à dire éclairée par des ondes planes. La figure 16 illustre la géométrie de l'interféromètre. L'onde plane incidente est réfléchie et transmise une multitude de fois.
éclairée par une source monochromatique à l'infini, c'est à dire éclairée par des ondes planes. La figure 16 illustre la géométrie de l'interféromètre. L'onde plane incidente est réfléchie et transmise une multitude de fois.
On note
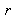 et
et
 les facteurs de transmission en amplitude des ondes aux interfaces air-verre. Le coefficient de réflexion en intensité
les facteurs de transmission en amplitude des ondes aux interfaces air-verre. Le coefficient de réflexion en intensité
 est très grand, de l'ordre de 99%, de sorte qu'on ne considère pas ici le cas simple de la lame à faces parallèle où on ne considère que les deux premiers rayons (voir figure 5). Par ailleurs, les coefficients de transmission et réflexion sont identiques pour les deux dioptres. Les angles
est très grand, de l'ordre de 99%, de sorte qu'on ne considère pas ici le cas simple de la lame à faces parallèle où on ne considère que les deux premiers rayons (voir figure 5). Par ailleurs, les coefficients de transmission et réflexion sont identiques pour les deux dioptres. Les angles
 et
et
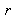 sont liés par la relation de Descartes
sont liés par la relation de Descartes
 . La différence de chemin optique entre deux ondes consécutives en transmission, est égale à [
] :
. La différence de chemin optique entre deux ondes consécutives en transmission, est égale à [
] :
En réflexion, nous avons
En transmission, le déphasage entre deux ondes consécutives est donc :
En sortie de la lame, en réflexion ou transmission, l'amplitude complexe est égale à la somme de toutes les ondes transmises ou réfléchies par la lame. Il suffit d'écrire l'amplitude des ondes qui interfèrent en prenant comme origine des phases la première onde
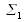 . Considérons que l'onde incidente est plane, polarisée suivant
. Considérons que l'onde incidente est plane, polarisée suivant
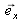 , de vecteur d'onde
, de vecteur d'onde
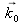 , nous avons simplement :
, nous avons simplement :
Après la traversée de la lame, on a :
pour
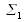 :
:
car l'onde traverse les deux dioptres
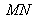 et
et
 en
en
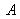 et
et
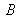 .
.
pour
 :
:
car double traversée de l'interface air-verre en
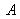 et
et
 et double réflexion à l'interface en
et double réflexion à l'interface en
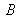 et
et
 et déphasage
et déphasage
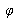 par rapport à la première onde ;
par rapport à la première onde ;
pour
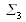 :
:
car double traversée en
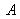 et
et
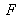 et quatre réflexions en
et quatre réflexions en
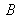 ,
,
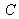 ,
,
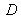 ,
,
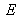 ce qui correspond à un déphasage de
ce qui correspond à un déphasage de
 par rapport à la première onde.
par rapport à la première onde.
Par récurrence, on constate que pour
 :
:
L'amplitude complexe totale en sortie de la lame résulte de la sommation de toutes les amplitudes :
On pose
 et
et
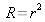 ,
,
 et
et
 sont les facteurs de transmission et réflexion en flux optique (ou puissance, ou énergie).
sont les facteurs de transmission et réflexion en flux optique (ou puissance, ou énergie).
La sommation des champs complexes donne :
On reconnaît une suite géométrique de raison
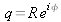 et de premier terme 1. Soit
et de premier terme 1. Soit
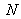 le nombre total de termes, on a pour la somme
le nombre total de termes, on a pour la somme
et compte tenu que
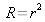 est inférieur à 1,
est inférieur à 1,
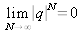 , il reste donc :
, il reste donc :
Le signal d'interférences est proportionnel à :
d'où :
que l'on écrira :
Comme
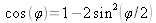 , on a :
, on a :
Posons :
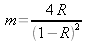 , et
, et
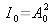
avec :
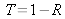
il vient :
Les valeurs minimales et maximales du signal sont :
et le contraste vaut :
Les courbes de la figure 17 illustrent le signal d'interférences
 en transmission en fonction de différentes valeurs du coefficient de réflexion
en transmission en fonction de différentes valeurs du coefficient de réflexion
 .
.
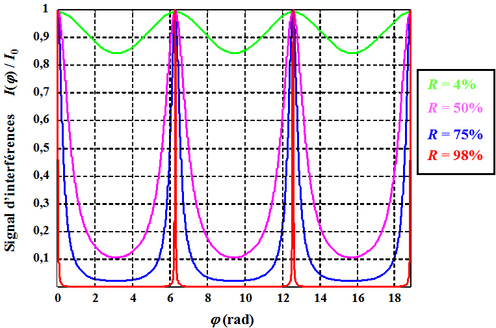
On constate que plus le coefficient de réflexion est élevé et plus le profil des franges s'éloigne du profil sinusoïdal classique. Pour
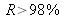 , le profil s'affine et constitue une fonction de filtrage dont les propriétés seront utilisées dans la partie « Étude de cas » de ce cours. Le cas
, le profil s'affine et constitue une fonction de filtrage dont les propriétés seront utilisées dans la partie « Étude de cas » de ce cours. Le cas
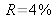 correspond au cas d'une lame de verre d'indice 1,5 traitée précédemment au paragraphe 3.1.
correspond au cas d'une lame de verre d'indice 1,5 traitée précédemment au paragraphe 3.1.
Supposons que la lumière incidente sur l'interféromètre de Fabry-Pérot soit polychromatique. Si le spectre de la lumière est composé d'un doublet très fin, les deux pics sont alors très proches, ils peuvent être discernés si ces derniers sont très fins comme les pics représentés en rouge figure 17.
L'intervalle spectral libre de l'interféromètre correspond à la variation de longueur d'onde
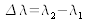 pour laquelle il y a superposition des pics consécutifs d'ordre
pour laquelle il y a superposition des pics consécutifs d'ordre
 pour la longueur d'onde
pour la longueur d'onde
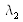 et d'ordre
et d'ordre
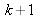 pour
pour
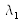 soit :
soit :
et :
d'où on déduit :
comme
 , on en déduit l'expression de l'intervalle spectral libre :
, on en déduit l'expression de l'intervalle spectral libre :
D'après l'expression de la fonction
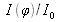 la largeur à mi-hauteur des pics de résonance de l'interféromètre est égale à :
la largeur à mi-hauteur des pics de résonance de l'interféromètre est égale à :
A partir de ces deux expressions on définit la finesse de l'interféromètre par :
Ces paramètres sont illustrés sur la figure 18.

Le tableau 1 donne des valeurs des paramètres de modulation, contraste et finesse en fonction du coefficient de réflexion.
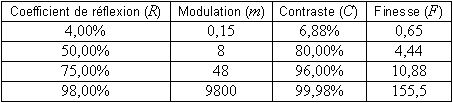
Le lecteur remarquera que dans le cas 4%, nous ne sommes plus en présence d'interférences à ondes multiples et qu'on retrouve le résultat vu plus haut relatif à une lame à faces parallèle traitée dans le cas des interférences à deux ondes (figure 5 et paragraphe 3.1).
L'interféromètre de Fabry-Pérot est couramment utilisé pour les analyses spectrales.
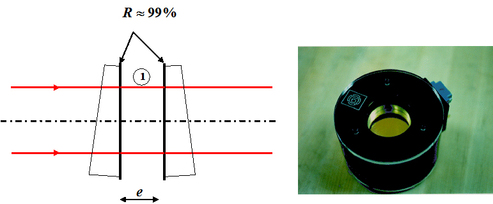
On l'utilise aussi souvent constitué d'une lame d'air d'épaisseur
 et de coins de verre dont les faces composants la lame de verre sont traitées pour que les coefficients de réflexion soient très élevés et proche de 1. On parle alors de « cale étalon ». Ce type de système est utilisé dans les cavités laser pour affiner spectralement et rendre la source monomode longitudinale, donc cohérente. La figure 19 présente le schéma de principe ainsi qu'une photographie d'une cale étalon.
et de coins de verre dont les faces composants la lame de verre sont traitées pour que les coefficients de réflexion soient très élevés et proche de 1. On parle alors de « cale étalon ». Ce type de système est utilisé dans les cavités laser pour affiner spectralement et rendre la source monomode longitudinale, donc cohérente. La figure 19 présente le schéma de principe ainsi qu'une photographie d'une cale étalon.