
Méthodes de reconstructions du front d'onde objet
Introduction
Deux méthodes sont présentées dans ce chapitre :
-
la reconstruction en phase et amplitude du champ complexe objet par transformée de Fresnel ;
-
et la méthode de reconstruction par convolution.
Toutes deux sont issues de l'intégrale de diffraction de Fresnel-Kirchhoff.
Reconstruction par transformée de Fresnel discrète
Considérons qu'à la place d'une ouverture diffractante classique nous ayons une transmittance discrétisée ; celle-ci représente un hologramme préalablement enregistré sur une matrice de pixels. Nous avons vu précédemment que l'onde objet est restituée par diffraction de l'onde référence sur le support holographique. Afin d'obtenir les informations de phase et d'amplitude du champ initial, il faut maintenant simuler la diffraction de l'onde de référence incidente sur la matrice transmittance.
L'intégrale de diffraction de Fresnel est discrétisée en remplaçant la double intégrale par une double sommation et les coordonnées du plan d'enregistrement sont échantillonnées avec un pas correspondant à celui de la matrice de pixels soit
 , où
, où
 et
et
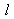 varient de 0 à
varient de 0 à
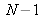 et de 0 à
et de 0 à
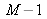 .
.
Par ailleurs, puisque le processeur ne pourra pas calculer une infinité de points du champ reconstruit, il faut également prendre en compte le caractère discret du plan image. En particulier, il est nécessaire de considérer la nature de l'intégrale de Fresnel : c'est une transformée de Fourier bidimensionnelle. Les règles classiques d'échantillonnage en temps et en fréquence qui s'appliquent au traitement numérique du signal classique sont également de rigueur dans notre cas. Pour une distance de reconstruction numérique
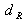 , la transformée de Fresnel discrétisée est écrite :
, la transformée de Fresnel discrétisée est écrite :
A ce stade, il faut noter que la prise en compte de l'onde de référence dans le calcul n'est pas obligatoire si elle est plane et uniforme
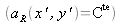 , contrairement au cas de la reconstruction physique par laser qui nécessite l'éclairage avec une onde de référence. Dans le cas d'une onde sphérique
, contrairement au cas de la reconstruction physique par laser qui nécessite l'éclairage avec une onde de référence. Dans le cas d'une onde sphérique
 , il faudra tenir compte de la courbure du front d'onde et multiplier
, il faudra tenir compte de la courbure du front d'onde et multiplier
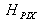 par un terme complexe adéquat.
par un terme complexe adéquat.
Discrétisation du plan reconstruit
D'après l'expression de la transformée de Fresnel discrète, les périodes d'échantillonnage apparentes de l'exponentielle donnant le caractère de Fourier de l'intégrale sont données par
Si le champ reconstruit est calculé sur le même nombre de points
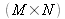 que le nombre de pixels du détecteur, le pas d'échantillonnage dans le plan image est égal à
que le nombre de pixels du détecteur, le pas d'échantillonnage dans le plan image est égal à
Par conséquent, l'échantillonnage dans le plan image est simplement
où
 et
et
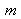 varient de
varient de
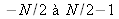 et de
et de
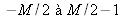 .
.
Le cas de l'extension du support avec des zéros (zero-padding) sera discuté dans un des paragraphes suivants. La version discrète de l'intégrale de Fresnel s'écrit finalement
Cette relation exprime le champ reconstruit aux coordonnées pixels
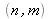 dans le plan image. A un facteur de phase près, le champ reconstruit est proportionnel à une transformée de Fourier bidimensionnelle discrète (FFT) du produit de l'hologramme numérisé par un terme de phase quadratique discrétisé.
dans le plan image. A un facteur de phase près, le champ reconstruit est proportionnel à une transformée de Fourier bidimensionnelle discrète (FFT) du produit de l'hologramme numérisé par un terme de phase quadratique discrétisé.
L'algorithme de reconstruction par transformée de Fresnel discrète est donné sur la figure 15.
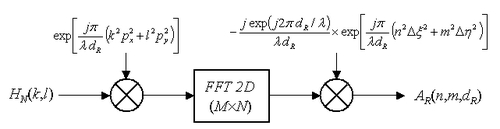
Si on choisit
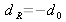 , alors l'ordre +1 sera au point dans le champ reconstruit, si en revanche on choisit
, alors l'ordre +1 sera au point dans le champ reconstruit, si en revanche on choisit
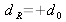 , la mise au point sera sur l'ordre - 1.
, la mise au point sera sur l'ordre - 1.
Contrainte sur la distance de reconstruction
Le lecteur notera que l'application de cet algorithme nécessite de programmer une version discrète du terme de phase quadratique de la transformée de Fresnel. L'échantillonnage de cette fonction complexe oscillante se doit de respecter les conditions de Shannon.
Pour ce faire, il suffit de considérer le contenu fréquentiel de la fonction en termes de fréquences spatiales [ ]. Considérons la phase du terme quadratique :
Les fréquences spatiales locales sont données par
donnant
Le terme quadratique est un signal à caractère non stationnaire puisque ses fréquences
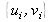 varient avec les variables d'évolution
varient avec les variables d'évolution
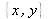 . En théorie, son énergie est infinie.
. En théorie, son énergie est infinie.
Cependant, le signal doit être considéré sur un support borné qui est l'espace pixel du détecteur. Le fait de limiter son horizon d'évolution impose de limiter son énergie et son contenu fréquentiel. L'étendue de x et y est bornée par
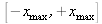 et
et
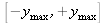 qui correspondent à l'étendue spatiale de l'enregistrement (
qui correspondent à l'étendue spatiale de l'enregistrement (
 pixels de pas
pixels de pas
 , capteur de taille
, capteur de taille
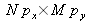 ), soit
), soit
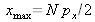 et
et
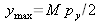 .
.
Ainsi, les fréquences spatiales maximales du signal sur ce support sont données par :
Sur l'espace détecteur, la bande passante spatiale bilatérale du terme quadratique est donc
La bande passante diminue donc lorsque la distance augmente. Le théorème de Shannon impose
Comme le pas des pixels est imposé par la technologie utilisée, la distance
 minimale respectant Shannon est donnée par
minimale respectant Shannon est donnée par
Le tableau 2 récapitule les distances minimales en fonction des paramètres d'acquisition.
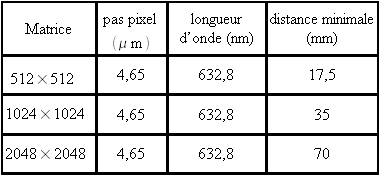
Ce résultat impose une distance minimale pour la reconstruction par transformée de Fresnel.
Expression de l'ordre + 1 numérique
Le calcul analytique du champ diffracté dans l'ordre +1 doit tenir compte de la surface active des pixels, du défaut de mise au point numérique et d'éventuelles aberrations de la surface d'onde de référence. Le calcul n'est pas détaillé dans le cadre de ce cours et on se contente de donner le résultat principal dans le cas où le pixel est infiniment ponctuel
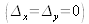 et pour
et pour
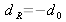 où on a
où on a
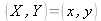 .
.
A partir de l'équation de la transformée de Fresnel discrète, on montre que le champ diffracté numériquement dans l'ordre +1 est donné par :
avec la fonction d'élargissement
et
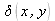 est la distribution de Dirac bidimensionnelle. L'ordre +1 est donc localisé aux coordonnées
est la distribution de Dirac bidimensionnelle. L'ordre +1 est donc localisé aux coordonnées
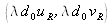 dans le plan reconstruit. Ces coordonnées dépendent des fréquences spatiales de l'onde de référence et de la distance de reconstruction.
dans le plan reconstruit. Ces coordonnées dépendent des fréquences spatiales de l'onde de référence et de la distance de reconstruction.
Ainsi que nous l'avions vu au paragraphe « Formation de l'image dans l'ordre +1 », l'objet reconstruit est également convolué par une fonction d'élargissement
 qui est liée à la largeur du capteur. Cette fonction est la fonction de filtrage de la transformée de Fourier discrète bidimensionelle. Sa forme mathématique apparaît très différente de celle de la fonction
qui est liée à la largeur du capteur. Cette fonction est la fonction de filtrage de la transformée de Fourier discrète bidimensionelle. Sa forme mathématique apparaît très différente de celle de la fonction
 , cependant, son profil est similaire à un sinuscardinal à deux dimensions.
, cependant, son profil est similaire à un sinuscardinal à deux dimensions.
Cette fonction impose la résolution intrinsèque en holographie numérique de Fresnel. Son interprétation est simple :
 est une tache de diffraction numérique d'une ouverture rectangulaire de largeur
est une tache de diffraction numérique d'une ouverture rectangulaire de largeur
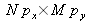 de transmittance uniforme. La fonction de résolution est représentée graphiquement en module sur la figure 16 pour les valeurs numériques suivantes :
de transmittance uniforme. La fonction de résolution est représentée graphiquement en module sur la figure 16 pour les valeurs numériques suivantes :
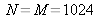 ,
,
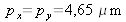 ,
,
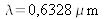 et
et
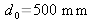 .
.
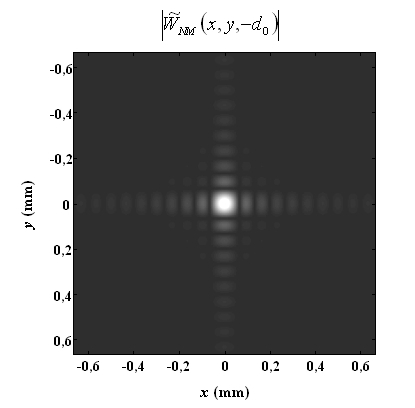
Selon le critère de Rayleigh, cette fonction a des largeurs horizontale et verticale égales à
Ces quantités fixent la résolution dans le plan image. La résolution spatiale est donc proportionnelle à la distance d'enregistrement et inversement proportionnelle à la largeur du capteur.
Une application numérique avec les valeurs ci dessus donne
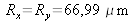 . En comparaison avec l'application numérique avec la plaque argentique de
. En comparaison avec l'application numérique avec la plaque argentique de
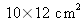 , la résolution spatiale est 21 à 25 fois moins élevée.
, la résolution spatiale est 21 à 25 fois moins élevée.
Suppression des ordres parasites
L'algorithme de la figure 15 peut être appliqué directement avec l'hologramme enregistré. Dans ce cas, le champ reconstruit contiendra systématiquement les trois ordres de diffraction. En 1997 [ ], Yamaguchi propose d'appliquer les techniques de démodulation de franges par décalage de phase à l'hologramme numérique. L'idée est que l'hologramme étant une composition interférométrique à deux ondes, il est possible d'extraire l'ordre utile par application d'un décalage de phase à l'onde de référence.
Notons
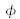 le décalage de phase appliqué à l'onde de référence qui s'écrit maintenant
le décalage de phase appliqué à l'onde de référence qui s'écrit maintenant
et choisissons 4 valeurs du déphasage
alors puisque H s'écrit aussi
nous pouvons extraire des quatre hologrammes enregistrés la phase du champ objet diffracté
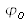 et son amplitude
et son amplitude
 et calculer l'ordre +1 qui correspond au terme
et calculer l'ordre +1 qui correspond au terme
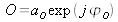 . En effet, en tout point où l'hologramme est enregistré :
. En effet, en tout point où l'hologramme est enregistré :
et
Puis, il suffit d'appliquer l'algorithme de la figure 15 à l'ordre +1 pour former uniquement l'image de l'objet initial. Cette méthode est efficace pour éliminer l'ordre +1, en revanche elle est gourmande en enregistrements puisqu'il faut 4 hologrammes pour retrouver l'objet.
Cas du zéro padding
Le lecteur remarquera que le pas d'échantillonnage de l'espace image dépend du nombre de points de la reconstruction, de la longueur d'onde, du pas des pixels et de la distance de reconstruction. Il n'y a donc pas d'invariance du pas d'échantillonnage lors de la reconstruction par transformée de Fresnel directe.
Comme nous l'avons évoqué au cours de l'un des paragraphes précédents, le calculateur estimera le champ diffracté sur un nombre fini de points. Le calcul de la transformée de Fresnel discrète de l'hologramme peut-être effectué sur
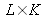 points tels que
points tels que
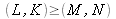 .
.
-
Si
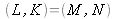 alors l'interférogramme brut est utilisé pour le calcul numérique de la transformée de Fresnel.
alors l'interférogramme brut est utilisé pour le calcul numérique de la transformée de Fresnel. -
Si
 , on se trouve dans le cas dit du « zero-padding » et cela revient à ajouter
, on se trouve dans le cas dit du « zero-padding » et cela revient à ajouter
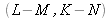 zéros à la matrice de pixels.
zéros à la matrice de pixels.
Fondamentalement, ce supplément de zéros n'ajoute pas d'information rationnelle, en revanche il modifie le pas d'échantillonnage du champ diffracté.
En effet, les pas seront maintenant donnés par :
L'échantillonnage dans le plan image est désormais
où
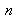 et
et
 varient de
varient de
 et de
et de
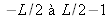 .
.
On a donc
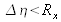 et
et
 . Il y a diminution du pas d'échantillonnage et ainsi augmentation de la « définition » du plan image.
. Il y a diminution du pas d'échantillonnage et ainsi augmentation de la « définition » du plan image.
Concrètement, ceci signifie que l'on observera plus de texture dans l'image : le zero-padding de l'hologramme aura pour conséquence de faire apparaître plus finement la structure des grains de speckle de l'image.
Toutefois, le zero-padding ne modifie pas la résolution intrinsèque qui est imposée par le nombre de pixels du détecteur et leur taille.
Reconstruction par convolution
Reprenons l'intégrale de diffraction de Fresnel-Kirchhoff exprimée dans un repère cartésien [ ] :
Cette intégrale est également une équation de convolution :
avec
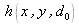 , la réponse impulsionnelle de l'espace libre, exprimée par
, la réponse impulsionnelle de l'espace libre, exprimée par
Dans le cadre des approximations de Fresnel, la réponse impulsionnelle devient
et le champ diffracté s'exprime sous la forme de la transformée de Fresnel que nous avons rencontrée au début de ce cours :
La réponse impulsionnelle a une fonction de transfert
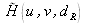 telle que
telle que
Appliquée à la reconstruction du champ objet à la distance
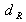 , à partir de l'hologramme
, à partir de l'hologramme
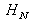 , la version discrète de l'équation de convolution est simplement :
, la version discrète de l'équation de convolution est simplement :
Il existe plusieurs manières d'appréhender le calcul pratique de cette relation. La plus simple est d'utiliser les propriétés de la transformée de Fourier : la convolution de deux fonctions peut-être traitée par la transformée de Fourier inverse du produit des transformées de Fourier de chacune des fonctions.
Cette propriété est exploitée en holographie numérique, étant donné que le calcul de transformées de Fourier discrètes présente un net avantage face à la convolution en temps de calcul (double sommation contre algorithmes optimisés).
Ainsi le champ reconstruit à la distance
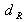 est calculé par application de l'équation suivante :
est calculé par application de l'équation suivante :
L'algorithme de reconstruction par convolution discrète est donné sur la figure 17.

Il est possible d'appliquer cet algorithme uniquement à l'ordre +1 extrait de l'hologramme par décalage de phase.
Le lecteur notera que les conditions de reconstruction évoquées au paragraphe précédent et concernant la distance minimale
 sont également valables dans ce cas. Si la réponse impulsionnelle exacte [
] est utilisée, on a
sont également valables dans ce cas. Si la réponse impulsionnelle exacte [
] est utilisée, on a
Considérons l'algorithme de la figure 17 : on utilise deux transformées de Fourier, l'une directe puis l'autre inverse. En conséquence, l'horizon d'observation du champ reconstruit est identique à celui de l'hologramme enregistré. Ceci signifie que le pas d'échantillonnage dans le plan image est identique au pas des pixels, soit
 et
et
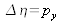 contrairement au cas du calcul direct pour lequel le pas dépend de la distance de reconstruction.
contrairement au cas du calcul direct pour lequel le pas dépend de la distance de reconstruction.
Cette méthode est donc indiquée pour les cas où le pas d'échantillonnage doit rester constant dans les différents plans reconstruits.
Balayage spectral par banc de filtres
Avec la méthode de la convolution numérique par FFT, l'horizon d'observation maximum est imposé par la taille du détecteur matriciel. Si l'objet a une taille supérieure à celle de la matrice de pixel, il est nécessaire d'effectuer un balayage afin de reconstruire l'objet par morceaux adjacents. En terme de bande passante spatiale, ceci signifie que la bande passante de la réponse impulsionnelle n'est pas suffisante pour couvrir la bande spatiale occupée par l'objet. Dans ce cas, la mise en œuvre de la reconstruction par convolution nécessite de programmer un banc de filtres dont la vocation est d'effectuer le balayage spectral nécessaire à la reconstruction de l'objet en entier.
Le nombre de balayages est fonction de la bande passante du filtre. Les relations espace métrique/fréquence spatiale montrent qu'à une fréquence spatiale de l'hologramme égale à
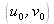 correspond une localisation dans l'objet reconstruit égale à
correspond une localisation dans l'objet reconstruit égale à
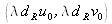 . La bande passante de la réponse impulsionnelle permet de reconstruire en une seule opération un domaine, égal à
. La bande passante de la réponse impulsionnelle permet de reconstruire en une seule opération un domaine, égal à
 en horizontal et égal à
en horizontal et égal à
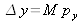 en vertical. Si l'objet est d'étendue
en vertical. Si l'objet est d'étendue
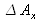 supérieure à
supérieure à
 le nombre de balayages en horizontal est donné par le rapport des bandes spectrales, soit
le nombre de balayages en horizontal est donné par le rapport des bandes spectrales, soit
Il est simplement égal au rapport taille objet / taille détecteur. Il existe une relation similaire en vertical avec
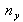 .
.
Si le spectre de l'onde objet diffractée est localisé aux cordonnées fréquentielles
 , les fréquences spatiales du banc de filtres sont données dans les deux directions par
, les fréquences spatiales du banc de filtres sont données dans les deux directions par
avec
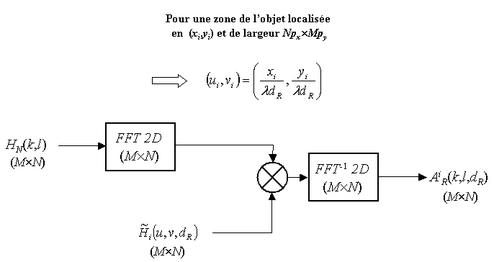
L'algorithme correspondant au balayage spectral est donné figure 18.
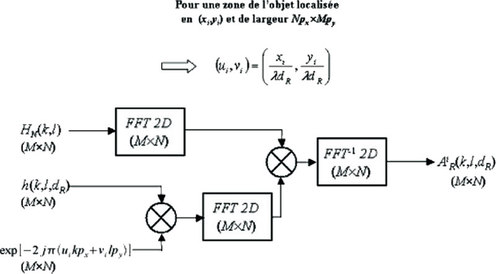
L'architecture traduit les propriétés de la transformée de Fourier quant au décalage spectral induit par des modulations dans l'espace direct.
Pour reconstruire une région de l'objet centrée aux coordonnées
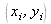 et d'étendue égale à la largeur du capteur
et d'étendue égale à la largeur du capteur
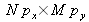 , on calcule la fréquence spatiale centrale associée à la zone, soit
, on calcule la fréquence spatiale centrale associée à la zone, soit
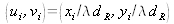 . Le filtre spectral associé à cette zone doit donc être centré dans le spectre de l'hologramme. Le centrage spectral s'effectue alors par modulation de la réponse impulsionnelle de l'espace libre en calculant numériquement
. Le filtre spectral associé à cette zone doit donc être centré dans le spectre de l'hologramme. Le centrage spectral s'effectue alors par modulation de la réponse impulsionnelle de l'espace libre en calculant numériquement
Ainsi, la fonction de transfert associée à la réponse impulsionnelle modulée par la fréquence spatiale de la zone spectrale est :
Cette fonction de transfert, multipliée par le spectre de l'hologramme, ne conserve que la zone spectrale d'intérêt. On peut ainsi reconstruire par balayage avec le banc de filtres la totalité de l'objet.
Plus la taille de l'objet est grande par rapport à celle du capteur plus il faut calculer de filtres et plus la reconstruction est longue. Par ailleurs, l'image finale est obtenue par juxtaposition des morceaux adjacents reconstruits : la taille de l'image de l'objet est donc maintenant
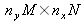 pixels. Si le nombre de balayages impose une taille d'image finale supérieure à
pixels. Si le nombre de balayages impose une taille d'image finale supérieure à
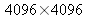 pixels, la place mémoire occupée sera considérable ce qui limitera les possibilités de traiter numériquement les résultats obtenus.
pixels, la place mémoire occupée sera considérable ce qui limitera les possibilités de traiter numériquement les résultats obtenus.
Autres stratégies
Il existe d'autres stratégies de reconstruction basées sur l'équation de convolution. A partir de l'expression des réponses impulsionnelles et des fonctions de transfert associées [ ], on distingue deux autres méthodes de reconstruction
-
banc de filtres à partir de la forme exacte de
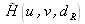 avec
avec
-
banc de filtres à partir de l'expression de
 dans les approximations de Fresnel, avec
dans les approximations de Fresnel, avec
Ces deux expressions sont à supports bornés pour la première et infini pour la seconde.
Compte tenu que les bandes spectrales sont finies en holographie numérique, ces deux expressions doivent être adaptées, d'une part, en limitant leurs étendues spectrales, d'autre part, en localisant ces fonctions de transfert en
 .
.
Ainsi elles deviennent respectivement
et
La figure 19 présente l'algorithme de reconstruction avec les fonctions de transfert.
La méthode s'apparente à celle présentée dans le paragraphe précédent, les nombres de balayages et tailles finales de l'image sont donc identiques.
Les méthodes de reconstruction numérique par convolution sont actuellement utilisées en microscopie holographique numérique : imagerie par polarisation ou par contraste de phase [ ] et en microscopie 3D [ , ]. En effet, la reconstruction dans différents plans de mise au point n'est judicieuse que si le pas d'échantillonnage de l'image reste constant.