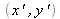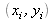Exercice auto-correctif
Préliminaires
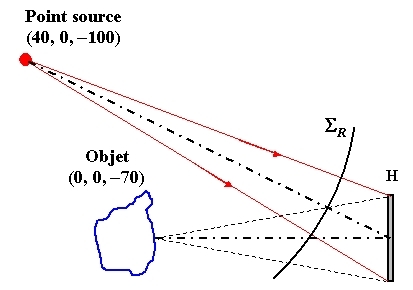
La géométrie du dispositif est décrite sur la figure 31, le repère étant celui de l'hologramme.
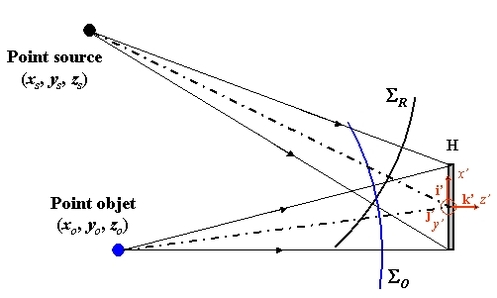
On considérera que le trou source est ponctuel, de longueur d'onde
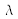 , localisé en
, localisé en
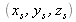 , et émet une onde sphérique divergente vers le plan de l'hologramme. L'objet sera considéré comme ponctuel et localisé en
, et émet une onde sphérique divergente vers le plan de l'hologramme. L'objet sera considéré comme ponctuel et localisé en
 .
.
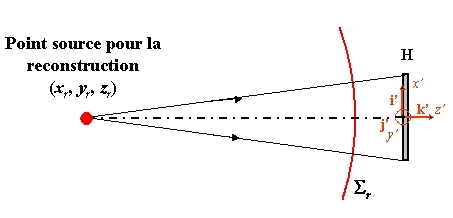
Pour le processus physique de reconstruction, on considérera que le trou source produisant l'éclairage de l'hologramme est localisé en
 et que sa longueur d'onde est
et que sa longueur d'onde est
 , avec
, avec
 .
.
Question
Exprimer l'amplitude complexe totale dans le plan de l'hologramme lors de l'enregistrement. En déduire l'expression de l'hologramme.
Question
Exprimer la transmittance de l'hologramme pour l'ordre +1 et pour l'ordre -1.
Question
Exprimer l'amplitude complexe issue de l'onde de reconstruction et incidente dans le plan de l'hologramme. En déduire les ondes transmises dans les ordres +1 et -1.
Question
Déduire du résultat précédent que les ondes dans les ordres +1 et -1 sont également des ondes sphériques de longueur d'onde
 issues d'un point image de coordonnées
issues d'un point image de coordonnées
 . En déduire les expressions de
. En déduire les expressions de
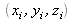 , dans chaque ordre, en fonction de
, dans chaque ordre, en fonction de
 ,
,
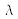 ,
,
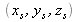 ,
,
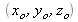 et
et
 .
.
Question
A partir des expressions des coordonnées du point source, déterminer le grandissement axial
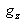 et les grandissements transversaux
et les grandissements transversaux
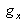 et
et
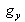 , pour la relation objet-image de l'ordre +1.
, pour la relation objet-image de l'ordre +1.
Question
Application numérique : on enregistre un objet situé en
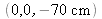 avec un laser hélium -néon dont le trou source est localisé en
avec un laser hélium -néon dont le trou source est localisé en
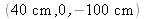 . La reconstruction est effectuée avec un laser NdYAG doublé dont le trou source est localisé en
. La reconstruction est effectuée avec un laser NdYAG doublé dont le trou source est localisé en
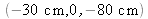 .
.
En déduire la position de l'image et le rapport des tailles objet/image.