Détermination de quelques caractéristiques d'un microscope

Il est possible de déterminer ou vérifier simplement quelques caractéristiques optiques d'une configuration objectif et oculaire donnée d'un microscope. Pour cela, il faut tout d'abord régler le microscope (comme indiqué précédemment par exemple) sur une préparation particulière appelée “micromètre objectif” qui est constituée d'une graduation calibrée, usuellement au 1/100ème de millimètre, gravée sur une lame de verre transparente et recouverte d'une lamelle de verre d'épaisseur 0,17mm standard.

Après réglage du microscope, on observe donc à l'œil derrière l'oculaire la graduation du micromètre fortement grossie. En regardant cette même image située à l'infini au travers d'une lunette à oculaire micrométrique préalablement calibrée angulairement sur un collimateur grand champ étalonné, il est possible de déterminer la taille angulaire de l'image de N intervalles du micromètre objectif (voir Fig.17 et Fig.18). Si l'écart entre deux graduations successives du micromètre objectif vaut 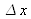, on en déduit immédiatement que la puissance totale du microscope vaut :

et étant respectivement exprimés en radian et en mètre, la puissance 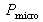en dioptrie.

Sur la figure 18, on peut lire que 4 intervalles de la graduation du micromètre (au 1/100mm), soit donc 0,040mm, vont de la graduation 11(±~½) à la graduation 87(±~½) de la lunette (en prenant dans les deux cas le bord gauche des traits du micromètre), soit donc 76±~1 intervalles angulaires élémentaires de la lunette. La calibration préalable de la lunette sur un collimateur étalonné ayant donnée qu'un intervalle du micromètre de la lunette représentait 0,0482°±1%, en en déduit que et la puissance totale du microscope vaut donc :

Par définition, le grossissement intrinsèque commercial du microscope est :

où dnorm représente la valeur normalisée de distance minimale de vision nette pour un observateur emmétrope standard, fixée à 0,25 m.

Des formules 2 et 3 on déduit que le grossissement intrinsèque commercial du microscope est de 400±10. Ce résultat est en parfait accord avec la valeur 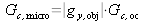attendue pour un objectif 40× et un oculaire ×10.

Il est ainsi possible de vérifier facilement, aux incertitudes de mesure près, les indications constructeur des optiques. Il est à noter que si l'oculaire est micrométrique, ce qui est le cas ici, on peut déterminer indépendamment le grandissement de l'objectif 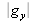par comparaison directe de la graduation de l'image du micromètre objectif avec la graduation du micromètre de l'oculaire, au 1/10ème de mm ici, et la puissance de l'oculaire 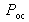en mesurant avec la lunette auxiliaire calibrée l'écart angulair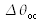e de 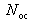intervalles des graduations du micromètre de l'oculaire, 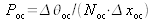. Les mesures et vérifications correspondantes à partir des informations de la figure 18 sont laissées en exercice au lecteur.

Le lien entre l'ouverture numérique objet 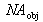et le diamètre du cercle oculaire peut être vu sur le tracé du rayon d'ouverture pour le point objet sur l'axe de la figure 2 de la partie cours. Le schéma ci-dessous en reprend les éléments essentiels.

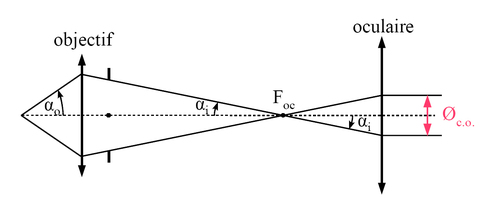
L'objectif et l'oculaire étant supposés aplanétiques pour leurs conjugaisons respectives, il est possible d'appliquer la relation des sinus d'Abbe (cf. cours de base d'optique géométrique). Celle pour l'objectif indique que les ouvertures numériques objet et image de celui-ci (ayant l'air d'indice 1 pour les deux milieux objet et image), et 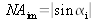, sont reliées au grandissement de l'objectif, par :

Par ailleurs, la relation des sinus d'Abbe pour la conjugaison foyer/infini (cf. cours de base d'optique géométrique ou la référence [ ]) de l'oculaire s'écrit, en remarquant que l'ouverture numérique objet pour l'oculaire est l'ouverture numérique image de l'objectif, par :

où 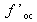est la distance focale image de l'oculaire.

En utilisant alors la relation reliant par définition le grossissement intrinsèque commercial de l'oculaire à sa focale ( ), on obtient :

On remarque que le diamètre du cercle oculaire est proportionnel à l'ouverture numérique objet du microscope et inversement proportionnel au grossissement intrinsèque commercial du microscope.

Le diamètre du cercle oculaire peut être mesuré à l'aide d'un viseur auxiliaire étalonné (cf. Fig.20 et Fig. 21a).

Sur la figure 21a, on note que le diamètre du cercle oculaire représente 19,5±~1 intervalles des graduations du viseur. Un étalonnage préalable du viseur sur un micromètre a permis de déterminer qu'un intervalle de la graduation du viseur représentait 42,9µm±~0,5%. Par conséquent, le diamètre du cercle oculaire vaut donc :

En utilisant la formule 6, on peut remonter à l'ouverture numérique de l'objectif, le grossissement intrinsèque commercial du microscope valant 400(±10), d'après la mesure du paragraphe précédent réalisée avec le même couple objectif/oculaire ; on obtient :

avec dnorm=250mm.

Cette valeur est tout à fait compatible avec l'indication 0,65 portée sur la monture de l'objectif 40× utilisé.