Densité de courant

Afin de décrire le comportement d'un semi-conducteur hors équilibre thermodynamique (soumis à une tension extérieure), nous devons étudier les courants résultants du déplacement des porteurs de charges que sont les électrons et les trous. Ce déplacement de charges se fait sous l'action d'une force dont l'origine peut être un champ électrique ou un gradient de concentration de porteurs de charges. Dans le premier cas, le courant est appelé courant de conduction, dans le second il est appelé courant de diffusion. Par ailleurs, nous ne caractériserons pas directement le courant mais la densité de courant J, proportionnelle à ce dernier. La densité de courant se définie comme étant la quantité de charges qui traversent une unité de surface par unité de temps.

Lorsque les trous et les électrons baignent dans le champ électrique créé par la mise sous tension de la jonction, ils se déplacent et génèrent ainsi le courant de conduction :

Où n et p sont les densités de porteurs, q=1,602.10-19C la charge d'un électron, E le champ électrique de la jonction polarisée et µn et µp les mobilités respectivement des électrons et des trous.

D'autre part, lorsque les électrons ou les trous ne sont pas distribués uniformément dans le semi-conducteur, leur mouvement s'effectue dans un sens qui tend à uniformiser leur distribution spatiale. Le flux de porteurs et donc le courant de diffusion est proportionnel à leur gradient de concentration :

Où Dn et Dp sont les constantes de diffusion des deux types de porteurs.

La mobilité des électrons étant plus élevée que celle des trous, la relation d'Einstein montre que, pour un même gradient de concentration, le courant de diffusion des électrons est plus grand que celui des trous.

Relation d'Einstein :

Il est évident que le courant total est constant dans toute la jonction. Aussi, pour l'évaluer, choisissons une région permettant de simplifier les calculs. Cette région correspond aux parties neutres N et P. En effet, loin de la zone de déplétion le champ électrique 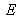en régime de faible injection est négligeable, ceci provenant de la conduction non nulle des semi-conducteurs. Le courant total est la seule somme des courants de diffusion des trous et des électrons. De plus, dans les zones neutres (hors zone de déplétion) la répartition spatiale des densités de porteurs majoritaires, c'est à dire les électrons coté N et les trous coté P, est constante. Or les courants de diffusion sont proportionnels au gradient de concentrations des porteurs, ainsi le courant total est généré par les porteurs minoritaires, c'est à dire les électrons coté P et les trous coté N. L'expression de la densité de courant total est donc:

Où xp (resp. xn) délimite la frontière de la zone de déplétion coté P (resp. N).

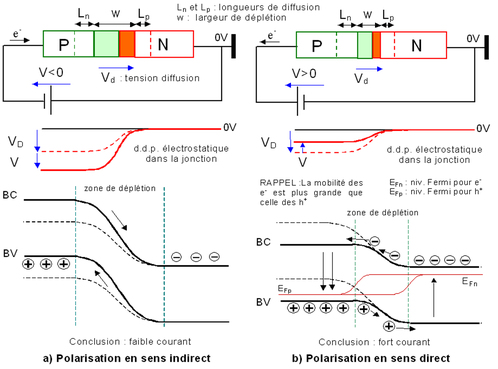
Afin d'exprimer J en fonction de la tension extérieure V, nous devons évaluer les densités de porteurs minoritaires np (=n(xp)) et pn (=p(xn)) dans les zones neutres. Pour ce faire, nous allons écrire les équations dites de continuité donnant l'évolution du nombre de porteurs au cours du temps.

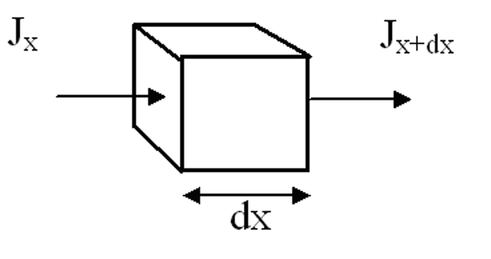
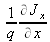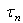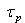Considérons un volume de semi-conducteur élémentaire de section unitaire et de longueur dx. La variation de porteurs par unité de temps dans cet élément de volume est la somme algébrique du nombre de porteurs qui entrent et qui sortent (traduit par l'apport de porteurs extérieurs ), de ceux qui se créent et de ceux qui se recombinent (traduit par les durées de vie et ). Ainsi, nous obtenons pour les trous et les électrons les équations de continuité suivantes :

Où np0 = n(xp) (resp. pn0 = p(xn)) est la densité d'électrons (resp. de trous) coté P (resp. N) pour la jonction non alimentée et 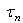, 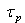les durée de vie respectives des porteurs dans les régions neutres.

Les équations de continuité à l'état stationnaire sont alors :

Où 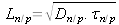sont les longueurs de diffusions des porteurs.

En notant les densités porteurs majoritaires nn0 (=ND) et pp0 (=NA), l'expression de la tension de diffusion nous permet de lier les densités de porteurs majoritaires aux porteurs minoritaires pour la jonction à l'équilibre :

Lorsque la jonction est alimentée la d.d.p. électrostatique devient Vd –V. Par analogie avec la jonction à l'équilibre, les densités de porteurs majoritaires et minoritaires sont liées par :

Où V est la tension de polarisation de la diode si l'on néglige les pertes ohmiques dans les semi-conducteurs dopés P et N

Dans le cadre de l'injection faible, les densités de porteurs majoritaires sont quasi constants entre l'état à l'équilibre et hors équilibre, on obtient alors pour variation de porteurs minoritaires :

Nous pouvons à présent résoudre les équations de continuité écrites à l'état stationnaire. Ces équations différentielles nécessites de connaître des conditions aux limites. Or les densités de porteurs minoritaires loin de la jonction n'ont pas été modifiées par l'alimentation de la diode, ce qui se traduit par : 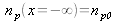et 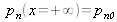. Les variations de densité de porteurs minoritaires sont alors exprimées en fonction de la position x dans la jonction hors zone de déplétion par :

En évaluant les densités de courants de diffusion aux limites de la zone de déplétion à l'aide des relations précédentes, on obtient la densité de courant totale :

avec