Relations entre grandeurs radiométriques

On présente ici quelques relations permettant de passer d'une grandeur du rayonnement à une autre, dans le cas de propagation dans un milieu homogène, c'est à dire d'indice constant. Elles sont valables longueur d'onde par longueur d'onde, c'est à dire applicables aux grandeurs spectriques dans le cas de rayonnements à spectres larges, et aux grandeurs intégrées des rayonnements quasi-monochromatiques. On peut aussi les appliquer aux grandeurs intégrées des rayonnements à spectre large, si la géométrie de ces rayonnements ne dépend pas de la longueur d'onde.

Pour ne pas alourdir l'écriture de ces relations, on ne précisera ni la longueur d'onde ni le cas considéré (grandeurs spectriques ou intégrées). D'autre part, on supposera que le milieu de propagation est parfait (le vide), l'influence du milieu étant abordée ultérieurement dans le cours.

On a vu que la grandeur radiométrique la mieux adaptée au rayonnement d'une source quasi-ponctuelle est son intensité I, qui permet de calculer le flux Φ (Ω) qu'elle émet dans un angle solide Ω, en supposant cette intensité constante (figure 5) :

Figure 5 : Angle solide d'un objet vu d'un point [zoom...]

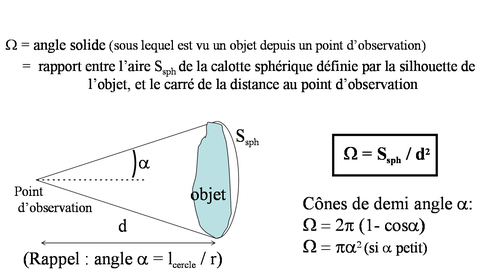
Si une source quasi-ponctuelle éclaire, sous un angle d'incidence θ', une petite surface d'aire Srécepteur qui est située à la distance d, l'angle solide Ω, sous lequel la surface se présente à la source, est le suivant :

et cette surface reçoit, de la part de la source, le flux suivant :

L'éclairement résultant de la surface est proportionnel à l'intensité de la source, au cosinus de l'angle d'incidence, ou facteur d'obliquité des rayons, et inversement proportionnel au carré de la distance, suivant la « loi de Bouguer » :

A une distance donnée de la source, le plan dont l'éclairement est maximal est celui qui est perpendiculaire aux rayons. Cette orientation, qui sert de référence à la distance considérée, définit le « plan de front ».

Si on a une source qui ne peut pas être considérée comme ponctuelle, on a vu qu'il faut en spécifier le rayonnement en chaque point de l'espace par sa luminance L en ce point, dans chaque direction d'intérêt. En partant de la définition de la luminance donnée plus haut, on peut écrire que le flux transporté par le rayonnement dans un petit angle solide Ω autour de la direction, au travers d'un petit diaphragme d'aire S centré sur le point et normal à la direction, est donné par :

En radiométrie optique, cette géométrie, définie par un petit diaphragme et un petit angle solide d'émission qui lui est normal, délimite un canal élémentaire, dénommé pinceau lumineux. Si le diaphragme, ou la surface de l'émetteur (si c'est lui qui joue le rôle de diaphragme), est orienté différemment par rapport à l'axe du pinceau, par exemple si sa normale fait un angle θ avec l'axe, l'aire de sa surface projetée dans cette direction, ou aire apparente, est alors Sapp(θ)=Scosθ et le flux transporté par le pinceau est alors :

Un pinceau, ou canal élémentaire constitué par une surface S, une direction θ et un angle solide Ω est défini par son étendue géométrique G=SΩcosθ exprimée en m2 sr.

On peut aussi délimiter un pinceau par deux diaphragmes, de surfaces respectives S et S', séparés d'une distance d (avec S et S'<<d2) et avec des normales faisant des angles θ et θ' avec l'axe (droite joignant les centres de S et de S'). Dans tous les cas, on exprime l'étendue géométrique d'un pinceau de l'une ou l'autre des trois façons suivantes, qui sont équivalentes (figure 6) :

où Ω' est l'angle solide sous lequel le second diaphragme voit le premier. Cela veut dire que chaque zone du diaphragme S éclaire S' en entier et que chaque point de S' reçoit de la lumière de tous les points de S.

Figure 6 : Etendue géométrique d'un pinceau lumineux [zoom...]

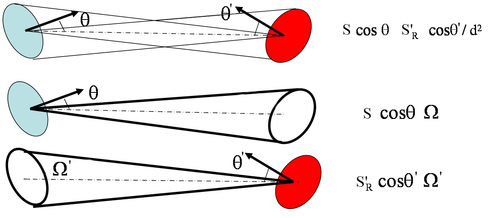
On en déduit que l'éclairement d'un élément de surface recevant de la lumière sous un angle d'incidence θ', par un pinceau d'angle solide (faible) Ω' et de luminance L, est le suivant :

Qu'advient-il du flux émis par une surface émissive dans un pinceau dont on augmente la divergence, sans modifier l'aire de la surface émettrice ni la luminance ? le pinceau, qui était initialement étroit, se transforme progressivement en un faisceau étendu.

Comme pour un pinceau, on attribue au faisceau une étendue géométrique dont la valeur est obtenue en sommant celles des pinceaux qui le composent. On réalise que, si on décompose le faisceau en un ensemble de pinceaux élémentaires d'angles solides identiques à partir de l'émetteur, leur étendue géométrique décroît en fonction de leur éloignement à l'axe du faisceau, par le fait que la section droite initiale de chaque pinceau est égale à Scosθ. Dans la mesure où les rayons sortent de la surface émissive sous des obliquités différentes, on conçoit que l'étendue géométrique d'un faisceau étendu n'est pas proportionnelle à sa surface émissive et à son angle solide. Comme le flux transporté dans un faisceau étendu est la sommation des flux transportés par ses pinceaux, on obtient, dans le cas d'un faisceau à luminance uniforme :

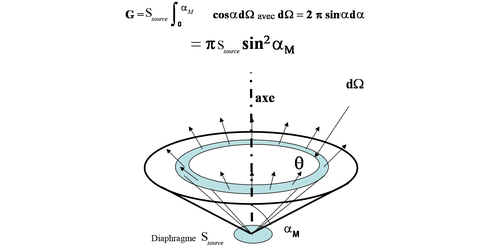
On donne ci-dessous l'étendue géométrique d'un faisceau étendu de forme simple, rencontré très souvent en optique, à savoir celle du faisceau défini par une surface émissive plane qui rayonne à l'intérieur du cône circulaire centré sur sa normale et de demi-angle au sommet 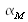 (figure 7) :

Si la surface émissive rayonne dans le demi-espace complet, soit un angle solide de 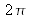sr, l'étendue géométrique de son faisceau est :

De façon similaire, un faisceau focalisé sur un détecteur de surface Sdét , dans un cône de demi angle au sommet 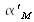centré sur l'axe, a pour étendue géométrique

Si le faisceau couvre le demi espace 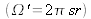, son étendue géométrique est alors :

Figure 7 : Etendue géométrique d'un faisceau défini par un diaphragme plan et un cône, ouvert, symétrique autour de son axe [zoom...]

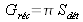
Si la luminance n'est pas constante à l'intérieur du faisceau, on ne peut plus écrire que 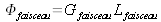, et l'étendue géométrique du faisceau perd de son intérêt au niveau du calcul du flux transporté par le faisceau.