Notions élémentaires sur la propagation d'une onde à la rencontre d'un dioptre
Une onde électromagnétique, monochromatique, plane, infinie et homogène se propage dans un milieu matériel homogène et isotrope dit incident (d'indice I). Elle tombe sur un dioptre plan infini constituant la séparation avec un milieu noté T où la vitesse de propagation de l'onde est différente.
La vitesse de propagation dans chacun de ces milieux est une constante optique du matériau et le caractérise suffisamment pour le problème posé. Dans un matériau indicé l, cette vitesse de phase,
, est égale au rapport de la pulsation de l'onde
et du module du vecteur de propagation kl.
Notons que lorsque l'on sort de cette approche optique pour traiter non plus le cas de la lumière mais des neutrons la vitesse v des particules avec masse est différente de cette vitesse de phase.
Pour la lumière, il est possible d'obtenir des faisceaux ayant une résolution spectrale presque parfaite (tels les LASERs) ce qui n'est pas le cas des faisceaux de neutrons. Pour les neutrons, la notion de paquet d'onde (Superposition d'ondes monochromatiques de fréquences légèrement différentes) est utilisée et il faut alors définir leur vitesse de groupe
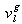qui est la quantité accessible expérimentalement.
Les premiers membres des équations suivantes définissent ces deux vitesses qui sont estimées respectivement à partir des relations de De Broglie et à partir de l'équation de la vitesse pour les neutrons introduite :
L'indice de réfraction absolu nI par le rapport des vitesses de phase de l'onde dans le matériau l notée
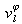et dans le vide notée C. Cet indice optique propre à la radiation monochromatique considérée vaut:
En comparant cette expression à celle de la vitesse de propagation d'une onde plane qui suit, on définit la relation entre l'indice et les permittivités:
où
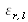et
correspondent aux perméabilités électriques et magnétiques relatives au vide, ainsi
et
où
et
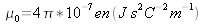sont propres au vide et
et
au matériau l et appelées permittivités absolues. Leur unité est le F.m-1. Pour simplifier l'écriture nous ne préciserons plus l'indice r dans la suite. Ainsi nous lions l'indice optique à ces constantes du matériau:
On introduit aussi l'indice relatif nIT du dioptre entre les deux milieux considérés et propre à une propagation allant du milieu I (incident) vers le milieu T (transmis). Il est égal au rapport des indices optiques absolus:
Pour les neutrons ayant une vitesse dans le vide
, nous obtenons: