Étude des interfaces et des couches minces par réflectivité des rayons X et Neutron

Utilisation des équations de Maxwell pour la continuité des champs au passage d'un dioptre

Rappelons les équations de Maxwell vérifiées par une onde dans un milieu matériel diélectrique parfait (c'est-à-dire de densités volumiques permanentes de charge et de courant j nulles) homogène et isotrope (soit de permittivité diélectrique et magnétique constantes).

Lorsqu'une onde se propage dans un milieu I et atteint un dioptre le séparant du milieu T, il apparaît une onde dans celui-ci. Les équations liant les champs de ces deux ondes sont dites équations de continuité et sont dérivées des équations de Maxwell. Elles s'appliquent au cas général d'une polarisation quelconque de l'onde électromagnétique incidente où les champs et 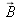ont simplement caractérisés par une composante normale (selon le vecteur unitaire perpendiculaire au dioptre ) et une composante tangentielle au dioptre (selon le vecteur unitaire coplanaire à ).

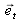En premier lieu considérons les flux des deux membres des deux premières équations de Maxwell à travers la surface Sa délimitée par le contour rectangulaire Ca de la Figure 1.

Figure 1 : Équations de continuité au dioptre plan [zoom...]

Nous introduisons le contour rectangulaire Ca qui délimite la surface Sa, et le volume cylindrique Vb de surface Sb, tous deux sont impliqués dans la démonstration des équations de continuité du champ électromagnétique à la surface de séparation des deux milieux indicés I et T. La hauteur des deux constructions est infiniment petite par rapport aux dimensions de leur bases, parallèles et de part et d'autre du dioptre.

L'équation de Maxwell-Faraday conduit à :

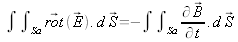
Selon la formule de Stokes appliquée au premier membre et puisque la dérivée de la fonction continue B l'est aussi, cette relation devient :

Le premier terme s'obtient en considérant uniquement les composantes tangentielles de dont les circulations sur et sont nulles et constantes sur et .

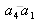Le flux de étant infiniment petit comparé à l'on obtient : . Cette relation est valable pour tout ce plan : .
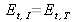Donnons également la relation obtenue de façon analogue avec l'équation Maxwell-Ampère :

La relation de Maxwell-Gauss 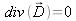et la conservation du flux magnétique , sont utilisées avec le volume d'intégration cylindrique décrit sur figure. En utilisant le théorème d'Ostrogradski on arrive aux égalités suivantes :

Seules les composantes normales au dioptre sont à considérer puisque le rapport des flux à travers les bases est infiniment grand devant celui à travers les surfaces latérales et D y est constant.

Ainsi les flux de chaque base doivent s'annuler ce qui donne la relation suivante :

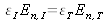
Des considérations similaires appliquées à l'équation de Maxwell conduisent à la deuxième équation suivante :

Lois de Snell-Descartes

Il n'est pas utile de spécifier la nature de l'onde tant est que celle ci est scalaire, i.e. entièrement caractérisée par une seule variable (complexe ou réelle). A la traversée du dioptre, les ondes peuvent à priori subir un changement de phase mais celui-ci doit être le même en tous points infiniment proches et de part et d'autre de l'interface. En un point du dioptre (z=0) cette variation de phase doit être la même pour les trois ondes I, R et T et l'on écrit :

En égalisant ces expressions on obtient les relations à vérifier en z=0 quel que soit :

De la seconde égalité on obtient la Première loi de la réfraction : le rayon réfracté est dans le plan d'incidence,
On en tire aussi la Seconde loi de la réfraction correspondant à l'égalité :

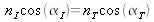
où et correspondent respectivement aux angles entre 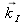et avec le dioptre.
On obtient aussi la Première loi de la réflexion : le rayon réfléchi est dans le plan d'incidence ;
Ainsi que la Seconde loi de la réflexion en réécrivant l'équation précédente au sein du seul milieu I et donc en considérant la réflexion comme une réfraction dans un milieu d'indice opposé. Elle s'énonce comme suit: les rayons incidents et réfléchis font des angles de droite égaux avec la normale au point d'incidence 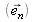. La direction de la réflexion est alors dite spéculaire et correspond à un angle sortant égal à l'angle incident .

Nous verrons que du vide (nI=1) vers un matériau (nT), la lumière transmise s'écarte toujours de la surface traversée puisque C est la vitesse limite (la matière est dite plus réfringente que le vide à la lumière (nT > nI)). Au contraire un faisceau de rayons-X se rapproche de la surface puisque les indices de réfraction aux rayons-X sont généralement voisins de 1 moins 10-6 (soit pratiquement 1). Le cas des neutrons est plus complexe puisque les deux situations sont possibles suivant les matériaux traversés (nT > nI ou nT < nI).

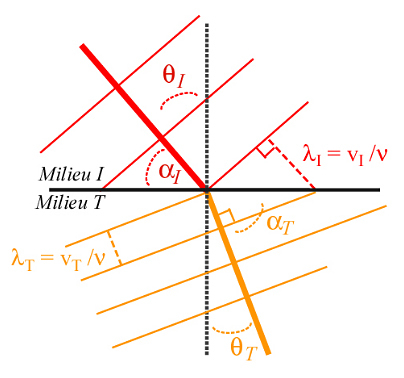
Figure 2 : Passage milieu I vers un matériau plus réfringent (milieu T) de la lumière visible [zoom...]

Les deux triangles rectangles représentés d'hypoténuse commune conduisent à la relation :

où v est la fréquence de l'onde qui reste constante au cours de ce processus élastique (conservation de l'énergie totale). La vitesse v et la longueur d'onde λ vont par contre être différentes dans chaque milieu.

Equation d'Helmholtz pour l'onde plane harmonique

La propagation du champ électrique et magnétique d'une onde (l) dans un milieu quelconque est régie par l'équation d'Helmholtz obtenue par combinaison des équations de Maxwell. Dans le cas où et :

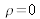Pour un milieu à propriétés continues (dit homogène) tel que sont de gradients nuls, l'équation d'Helmoltz se simplifie et on obtient :

et étant la dérivée seconde du champ par rapport au temps.

En pratique on peut considérer un matériau comme étant homogène lorsque ses caractéristiques affectant l'onde le parcourant ( 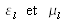) varient très peu sur des longueurs de l'ordre de la longueur d'onde et peuvent être considérées comme constantes à l'échelle macroscopique. Homogène n'implique pas isotrope.

Lorsque l'onde est sinusoïdale elle vérifie :

Les champs électriques (grandeur vectorielle) solutions de l'équation différentielle s'écrivent :

Ici l = I, R et T dénotent les champs incidents, réfléchi et transmis.

Notons que la séparation en trois ondes utilisée pour décrire ce phénomène est artificielle puisqu'elle ne correspond pas à une réalité physique. C'est en quelque sorte une représentation commode pour le calcul du champ électromagnétique dans le milieu I qui s'obtient par interférence (sommation en amplitude) des ondes I et R situées dans le milieu d'incidence.

Nous allons maintenant détailler le sens des différentes grandeurs utiles (représentées dans le plan complexe sur la figure suivante). Tout d'abord nous rappelons que selon un processus élastique la dépendance temporelle est connue et définie par la pulsation w de l'onde qui est conservée ( 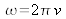). Pour simplifier l'écriture, on peut éliminer cette dépendance en définissant l'amplitude complexe (appelée "phasor" par les anglophones). Ici Al est l'amplitude réelle et est la phase indépendante du temps qui est incluse dans le facteur de phase. La dépendance temporelle de l'onde se restaure simplement quand on en a besoin selon , où 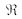désigne la partie réelle.

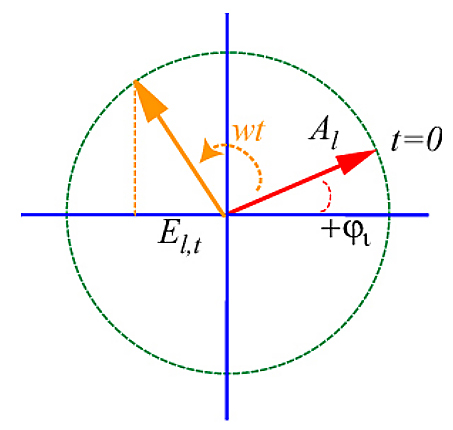
Figure 3 : Illustration de la phase d'une onde progressive représentée par un nombre complexe [zoom...]

La quantité El est représentée dans le plan complexe par un vecteur de longueur Al tournant dans le sens des aiguilles d'une montre autour de l'origine à la vitesse angulaire ω (aussi notée w) à partir d'une origine définie pour t=0 à laquelle ce vecteur forme l'angle.

Etudions le cas d'une onde plane polarisée linéairement dont le champ électrique est perpendiculaire au plan d'incidence (polarisation dite "TE" pour Transverse Electrique, notée " s " ou "⊥"). Une seconde polarisation souvent étudiée correspond à l'onde dont le champ magnétique est perpendiculaire au plan d'incidence (polarisation dite "TM" pour Transverse Magnétique, notée " p " ou "//").

Notons qu'on peut toujours décomposer en une combinaison linéaire de ces deux polarisations (s et p) une onde polarisée de façon quelconque (voir figure 4).

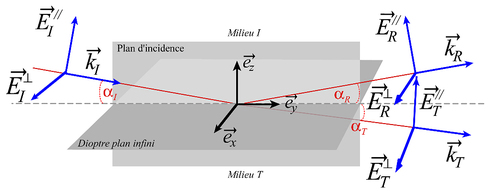
Figure 4 : [zoom...]

Figure 4 : Représentation des axes selon lesquels on décompose le champ électrique d'une onde de polarisation quelconque tombant sur le dioptre plan (z=0) qui sépare les deux milieux semi-infinis d'indices nI et nT. Les vecteurs 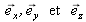définissent un trièdre direct orthonormé. Le plan dit d'incidence est soutenu par .

Aussi, il est possible de transposer au cas de la polarisation "p" tous les résultats que nous allons obtenir pour une polarisation "s" en raison des symétries respectées par les équations de Maxwell et qui conduisent aux substitutions suivantes :

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Notions élémentaires sur la propagation d'une onde à la rencontre d'un dioptreCoefficients de Fresnel en amplitude, réflectance r et transmitance t