Coefficients de Fresnel en amplitude, réflectance r et transmitance t

L'onde incidente "TE" pour Transverse Electrique (polarisée "s") est prise selon . Les variations de son champ électrique vectoriel sont :

De cette expression on peut identifier une famille de plans orthogonaux à la direction constituant les lieux où le champ électrique oscille en phase ( 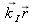est constant). Deux de ces plans consécutifs sont séparés par la longueur d'onde . La vitesse de phase qui définit la propagation équiamplitude le long de s'obtient selon l'équation différentielle suivante où intervient la coordonnée s colinéaire à :

Appliquons les relations générales que doit respecter cette onde à la traversée du dioptre représenté sur la figure ci-dessous. On choisit le référentiel tel que le vecteur de propagation de l'onde incidente ait uniquement deux composantes selon y et z :

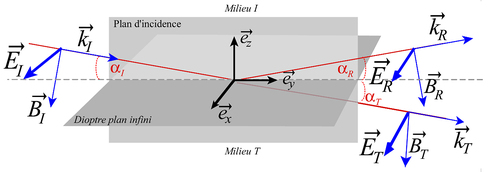
Selon les premières lois de Descartes les vecteurs d'ondes appartiennent au plan d'incidence contenant la normale au dioptre. Les vecteurs de diffusion des ondes réfléchie et transmise s'écrivent donc : avec l=R ou T.

Selon la deuxième loi dite de Snell-Descartes la réflexion est purement spéculaire, c'est-à-dire à un angle sortant égal à l'angle incident ( ). En considérant que ce processus est élastique et selon la conservation de la composante tangentielle des vecteurs d'onde , nous obtenons :

La continuité de la composante du champ électrique tangentielle (au dioptre) s'écrit (selon Fresnel) :

Selon les expressions des vecteurs de diffusion, nous obtenons :

Cette relation étant satisfaite sur toute l'interface plane ( 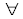x,y en z=0), nous obtenons :

Cette dernière relation étant connue sous le nom de loi de Snell-Descartes. On devrait alors préciser pour un dioptre défini, qu'un angle de réfraction différent existe pour chaque angle d'incidence, soit .

La composante tangentielle du champ magnétique est aussi conservée à la traversée du dioptre et nous obtenons son expression selon la relation de Maxwell liant le champ magnétique au champ électrique :

Notons qu'une onde plane est dite transverse car les vecteurs ou 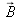sont dans le plan d'onde qui est perpendiculaire à la direction de propagation. Ces deux vecteurs sont aussi perpendiculaires entre eux et forment un trièdre trirectangulaire direct tel que pour notre cas:

Par projection sur l'axe 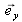nous obtenons la composante tangentielle de 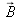égale à :

Sa continuité au passage du dioptre s'écrit :

ce qui conduit à

On obtient ainsi les équations de Fresnel en introduisant les coefficients de réflexion (r) et de transmission (t).

L'équation se réécrit :

qui devient :

En combinant les relations pour r et pour t, nous obtenons les relations de Fresnel (~1823) qui peuvent se simplifier en utilisant la relation de Snell-Descartes conduisant aux seconds membres ci-desous :

Le même raisonnement appliqué au cas d'une onde de champ électrique polarisé parallèlement au plan d'incidence (dite polarisée "p") conduit à :

Dans la théorie électromagnétique, cette grandeur correspond à l'intégration du vecteur flux d'énergie de l'onde 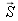sur la surface fermée de mesure de vecteur unité définissant sa normale . Donnons l'expression de l'intensité générale ( et 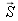sont colinéaires) et son expression développée au cas particulier des ondes planes :

et pour une onde plane :

Pour un diélectrique parfait ( 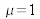), le module de ce vecteur vaut 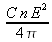et correspond à l'intensité lumineuse en J.s-1.m-2 se propageant suivant . Pour le problème que nous traitons, estimons la quantité d'énergie au dioptre par unité de surface et de temps qui est notée J. C'est un éclairement qui a l'unité d'une intensité et qui correspond au flux par surface commune aux trois faisceaux considérés dans cette approche (I, R et T).

Les quantités auxquelles nous nous intéressons étant ainsi complètement définies :