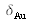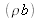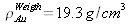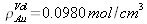Détermination de la densité électronique et de l'épaisseur d'une couche mince d'or par réflectivité spéculaire des rayons-X
Nous allons déterminer l'épaisseur d'une couche mince d'or déposée sur un substrat de verre (type SiO2). La figure présente la courbe de réflectivité X mesurée en bleu et la courbe rouge est obtenue suivant un calcul dynamique de la réflectivité utilisant l'algorithme de Parratt introduit dans le cours. En ajustant les paramètres du modèle on obtient la courbe rouge conduisant à l'épaisseur, la rugosité et la densité électronique de la couche d'or ainsi que la densité électronique du substrat et sa rugosité (la prise en compte de la rugosité dans le calcul n'est pas présentée dans ce chapitre du cours).
Les Paramètres d'ajustement du modèle qui sont fixés aux valeurs attendues sont marqués d'une étoile dans le tableau. Ils sont calculés pour une énergie de 8050.9122 eV (soit
), soit
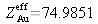électrons effectifs (l'or a 79 électrons mais la correction anomales
à Z diminue la valeur effective du nombre d'électrons participant à l'interaction avec le rayonnement X).
Question
Calculer à partir des paramètres issus de l'analyse de la réflectivité, les propriétés suivantes de la couche d'or :
-
L'angle critique en degrés à partir du vecteur de diffusion critique de la couche d'or.
-
Sa densité de longueur de diffusion (en
) à partir de son angle critique. -
Sa densité électronique en
. -
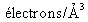Sa densité atomique.
![[zoom...]](javascript:window.open(%22../res/fig_12_E_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
Question
A partir de la réflectivité mesurée, il est possible de remonter assez précisément à l'épaisseur de la couche dense d'or simplement à partir de la période des oscillations. Dans le cas présent, on compte 7 oscillations entre l'angle d'incidence 1,040° et 1,809°. En déduire l'épaisseur de la couche d'or.