Population of "lower levels" at room temperature
In order to find out the efficiency of a laser transition, it is important to know if the lower level is occupied or not at thermodynamic equilibrium. For this, Boltzmann's Law is applied:
where
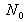is the population of the ground state whose energy is taken to be 0 and
is the population of the energy level
under consideration. To make this easier to use, “thermal” energy
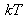can be converted into cm-1 thanks to the formula given in the note below. Thus, for a temperature of 300 K, kT=208 cm-1.
From the relation between frequency and energy level:
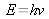, the relation between energy expressed in wavenumber and energy expressed in joule can be deduced:
E(J) = 100 h c E(cm-1)
By applying Boltzmann's Law, it can thus be shown that the lower levels for the transitions at 1064 nm and 1320 nm are not occupied because they are situated several thousands of cm-1 from the ground state: the ratio E1/kT is thus very low
On the other hand, the lower level (Z5) for the transition at 946 nm has an energy of the same order of magnitude as kT. 1.6% of the population of the ground state is found in the lower level. Thus, to invert the population, at least the same quantity of ions must be put into the upper level and this quantity cannot then be used for amplification by stimulated emission. This results in a loss of efficiency in comparison with the previous transitions.