Maxwell's formalism

In order to represent a wave, we must associate electrical 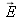and magnetic 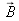fields to physical quantities which are a function of space 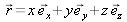and time t. Maxwell demonstrated that these fields are coupled in a given medium as described by the following equations (They are known as “Maxwell's Equations”) [1]:

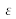where  is the permeability of the medium, is the permittivity of the medium, 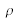is associated with the free charges and the medium's polarization charges, and 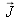is associated with the conduction currents and the medium's polarization currents. In a vacuum, we have 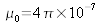and and 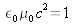, where stands for the propagation speed . In a linear, homogenous, and isotropic medium with no free charges we have 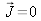, 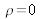and 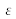 is a constant,.as is the case, for example, of unconstrained glass or air.

Maxwell's equations hence produce the propagation equations for magnetic and electrical fields, which are generally expressed as:

where 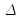is the Laplacian vector (we have ), n is the refractive index. This equation also holds for the magnetic field.

Note that all the components of , {Ex,Ey,Ez}, and 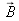,{ Bx,By,Bz} are subjected to the same propagation equation:

and also for {Ey, Ez, Bx, By, Bz}.

Therefore, it is possible to synthesize the behavior of these components by a single scalar wave 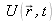defined by the propagation equation:

where 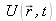represents any of these components {Ex, Ey, Ez, Bx, By, Bz}.

A rectilinear polarized wave in the x direction is written:

with:

If the wave propagation exhibits a spherical symmetry, the change in spherical coordinates produces the following wave equation:

where  .