Interferogram in polychromatic light
In the case of two waves that originate from a polychromatic source, the spectrum of the source no longer corresponds to a single ray located at wave number
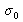(or also at
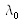wave length,
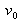frequency, or
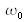angular frequency). The spectrum, or spectral energy density, denoted as
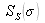, is composed of an envelope
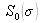centered on the average wave number
.
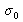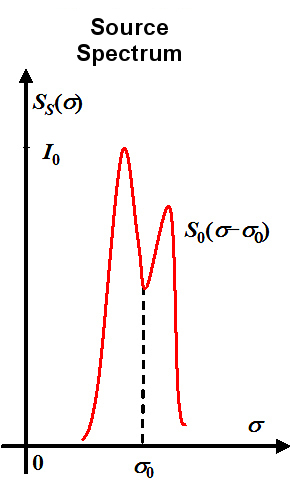
Figure 8 illustrates the spectral representation of the source.
![[zoom...]](javascript:window.open(%22../res/fig_08_C_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
According to paragraph B.4 "Interferences signal", the interference signal can be expressed as:
where:
where
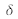is the difference in the optical path difference between the waves, and from now on becomes:
The interferogram (or fringe pattern) is written as an integral [2]:
The spectrum of the source, in other words the spectral representation of the source, is by nature real and zero for all values
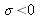. It follows therefore, that since
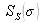is real:
where
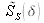is the Fourier transform of the spectral density, and we write:
This result, therefore, means that the interferogram observed in the presence of the polychromatic light is directly related to the Fourier transform of the source's spectrum.
Qualitatively, if the source has a narrow spectrum, then the interferogram will be large and spread out; and if the source has a very large spectrum, then the interferogram will be localized at
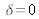. We express the spectrum in the following manner:
where
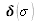is the Dirac distribution. We thus have:
At
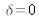, we have
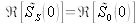and the distribution of intensity as a function of optical path difference
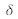becomes:
The cosine's term of modulation is referred to as the degree of temporal coherence. We note the degree of temporal coherence:
This result constitutes the Wiener–Kinchine Theorem [2]: it demonstrates that the degree of temporal coherence at point M on the screen is equal to the numerical value of the Fourier transform of the spectral energy density, calculated to the value of the optical path difference of point M. The degree of temporal coherence is normalized in such a way that
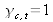if the source is monochromatic; if the source only emits a single wavelength, the temporal coherence is obviously perfect.