Young's slit experiment with monochromatic light

In this paragraph we will examine how to express as a function of the abscissa x of observation point M, of the distance a of the slits, and of the distance d0 from the slits to the observation screen. In this set-up, the distance d0 in meters is far larger than the distance between the axes a of the slits in millimeters. It is possible to consider that the distance F1M is equal to the distance MH, which is the same as identifying the cord F1H with the corresponding arc. 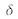Since the index of air is very close to 1, the optical path difference is equal to length F2H :

The distance d0 is also large for x, the angles     are small and slightly different from one another, so if 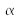  is expressed in radians:

i.e. by combining the last two equations:

and replacing 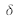  with its expression in relation (2), we obtain an expression for the interference signal:

The spatial period on the screen, referred to as interfringe distance is expressed as:

It represents the distance on the screen between two consecutive bright fringes or two consecutive dark fringes. If the distance a between the slits increases, the interfringe distance i diminishes; the interfringe distance also diminishes with the wavelength.

You can see an animation of these influences at the following website:

http://www.f-vandenbrouck.org/interference1.html

Since a, d0,  are constants for any given set-up, the site of the points that are in the same state of interference and have thus the same order of interference, verifies that:

Therefore, site of these points is constituted by a set of planes parallel to the constant abscissa. On the screen, these planes present rectilinear fringes that are parallel to each other (see figure 23).