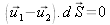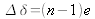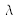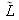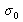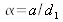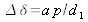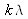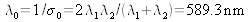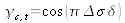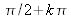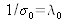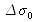Problem
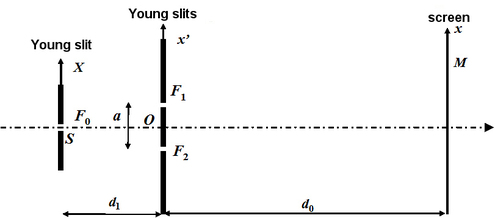
Let us consider two slits F1 and F2 made on an opaque screen that are infinitely narrow, vertical, and spaced by
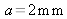 . They are illuminated by a point source S, monochromatic with a wavelength of
. They are illuminated by a point source S, monochromatic with a wavelength of
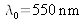 . The source slit S is equidistant to F1 and F2. The interference pattern is observed on a screen E, which is parallel to the slits and
. The source slit S is equidistant to F1 and F2. The interference pattern is observed on a screen E, which is parallel to the slits and
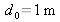 away from them.
away from them.
Question
Calculate the illumination on screen E. Determine the interfringe distance and the contrast.
Question
How does the preceding result change if S is replaced by a vertical, infinitely narrow slit F0 that is parallel to F1 and F2 ?
Question
What can be observed if we introduce a constant phase shift
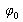 on one of the trajectories? At F1 we interpose a very thin glass plate with parallel faces, of index
on one of the trajectories? At F1 we interpose a very thin glass plate with parallel faces, of index
 . When this plate is placed on screen E, all of the fringes translate by
. When this plate is placed on screen E, all of the fringes translate by
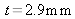 .
.
-
What is the direction of this translation?
-
How many fringes are affected by this?
-
Deduce the thickness e of the glass plate.
Question
We replace the plate with an absorbing screen with an optical density of 2
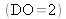 . Determine the new contrast.
. Determine the new contrast.
Question
We remove the density filter and now use a spatially incoherent source.
Describe the phenomenon that is observed if the source is polychromatic (white light).
Question
The source is
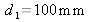 away from F1 and F2 and has a width of
away from F1 and F2 and has a width of
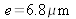 . What happens to the light at point M on screen E? How does the visibility vary with e ? What is the maximum width for which the decrease in contrast remains below 10% ?
. What happens to the light at point M on screen E? How does the visibility vary with e ? What is the maximum width for which the decrease in contrast remains below 10% ?
Question
We use as source a grid made up of slits that are parallel to F1 et F2. Determine the grid spacing and the width of the slits for which the contrast remains of the preceding value.
Question
The source is once again a slit reduced to F0 but the source of monochromatic light is replaced by a sodium vapor source, which has a spectrum essentially made up of two radiations with a wavelength of
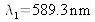 and
and
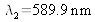 .
.
Find the energy spectral density function
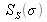 in terms of the average wave number
in terms of the average wave number
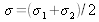 and the deviation of the doublet
and the deviation of the doublet
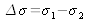 .
.
Find the illumination normalized for screen E.
Question
Carefully represent the previous function.
Question
What is the value of the interfringe?
Question
For which values of the optical path difference is there contrast cancellation?
Question
A source emits a spectral line with an energy spectral density function that can by described by a gaussian shape:
where
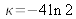 ,
,
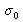 is the average wave number. The line is centered on the wavelength where
is the average wave number. The line is centered on the wavelength where
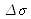 is the width at mid-height
is the width at mid-height
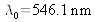 . The source has a spectral width of
. The source has a spectral width of
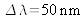 .
.
What is the value of
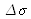 ?
?
Question
Find the normalized illumination for screen E.
Calculate the coherence length of the source.
Question
Carefully graph the normalized illumination.
Question
What is the value of the interfringe distance?
Question
Re-do the previous questions for the case of a two-wavelength sodium source, taking into account the physical nature of each line: the fact that each line is described by a gaussian shape. Assume
 as the width of each line, which corresponds to 300K of inhomogeneous broadening due to the Doppler effect, and
as the width of each line, which corresponds to 300K of inhomogeneous broadening due to the Doppler effect, and
 for the distance between the two lines.
for the distance between the two lines.
What are the values of
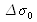 and
and
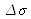 ?
?
Question
Recalculate the normalized illumination considering that each sodium doublet can be described by the Gaussian shape.
Graph the spectrum of the source and the obtained interferogram.