Different recording configurations

It is possible to record a hologram using various different configurations which sometimes move away from the basic principle of holography whilst keeping a strong correlation with holography as far as recording the interferometric pattern is concerned. A convergent or divergent lens between the object and the matrix sensor is often used. Generally, it is preferred that the reference wave is plane , so that its phase is simply written :

Diffraction using the Fresnel approximation requires that the finite distance between the object and the recording plane be taken into account. Figure 13 represents the recording device. The reference wave is plane and can follow the object wave axis for “in line” configuration recording or it can set up an angle with the object wave for “off axis” configuration recording. The device is the most widespread for the digital recording of interference patterns [].

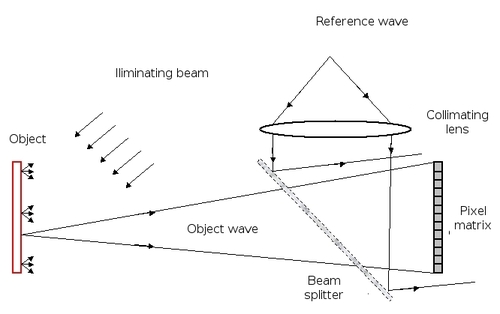
The distance between the object and the pixel matrix must follow the Fresnel conditions [].

The recording device, depicted in figure 14, sees the object placed in the focal plane of a convergent lens.

The role of the lens is to collimate the beam diffracted by the object. This configuration allows one to balance out the quadratic phase term by adjusting the transmittance pattern in the Fresnel diffraction integral. Thus, the effective distance between the object and the recording plane is infinite relative to the object and sensor apertures.

This configuration corresponds with the Fraunhofer conditions. Generally, the hologram is categorized as a Fourier hologram since a simple Fourier transform is sufficient to reconstruct the object field .