Conjugate planes, focal planes

A set of object points situated on a sphere with centre C going through A have, as an image, some points situated on a sphere of which the centre is C going through A' with the axial beam revolving around C. The spherical object surface has for an image a curved image surface. The fact that the images are not formed on a plane is an aberration named “field curvature”.

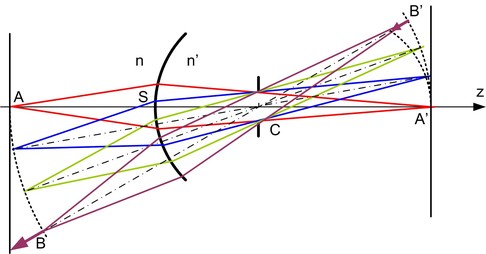
Following figure 16, if we displace an object point B situated outside the axis in the negative direction following the line BC through to the plane perpendicular to the axis going through A, its image B' moves in the same direction since gz is positive. This displacement increases the curvature of the image plane, the image of a plane therefore is not a plane.

With respect to paraxial approximation, we will neglect these curvatures because the angles are small as well as objects and images distances to the axis. The gap between the real position of the image and the plane going through A' if of second order relatively to the distance to the axis. Generally, paraxial approximation only keeps the terms of the first order.

In Paraxial approximation the image of a plane, is a plane.

Any object point to infinity has an image in the image focal plane, plane perpendicular to the axis going through F'.

Any point of the object focal plane, plane perpendicular to the axis going through F, has an image to infinity.