Spatial filtering

Filtering techniques are an important part of image processing systems, in particular when it comes to image enhancement and restoration. Here, we only consider linear and spatially invariant systems. We demonstrate that image g(x,y) resulting from the passing of image f(x,y) through such a system can be computed using a 2D convolution product with the system impulse response h(x,y),

with:

In this expression, the impulse response h(x,y) is defined as the system response to a bidimensional delta function,

The knowledge of this function fully characterizes the linear and spatially invariant system and allows calculating its response to any excitation. On a mathematical point of view, the bidimensional convolution product is commutative, associative, and distributive with respect to the addition. The delta function is the neutral element of this operator. One important consequence of those properties regards the combination of several linear and spatially invariant systems: the serial association of such systems is equivalent to having a unique linear and spatially invariant system whose impulse response is the convolution product of the individual impulse responses. The parallel association of several systems is equivalent to having a unique linear and invariant system whose impulse response is the sum of the individual impulse responses. In order to characterize the spectral properties of linear and spatially invariant systems, we now study the response of such a system when excited with a complex exponential function f(x,y):

Afin de caractériser les propriétés fréquentielles des systèmes linéaires invariants on étudie maintenant la réponse d'un tel système à une excitation sinusoïdale complexe f(x,y) ,

the quantities u and v represent the spatial frequencies along axes x and y. We now compute the response of system h(x,y) to signal f(x,y). By applying the convolution product to f:  :

we immediately obtain:

The response is therefore the product of the initial signal f(x,y) with a integral term depending only on h(x,y) and on the frequencies u and v.The output image is therefore an image of the same frequencies u and v. This term is the frequency response H(u,v) of the system h(x,y). H(u,v) exactly corresponds to the 2D Fourier transform of the impulse function h(x,y).

In numerous situations, determining the convolution product is facilitated by the use of the Fourier transform. Indeed, among the 2D FT properties previously listed, the one related to the convolution product directly applies to the case of linear and spatially invariant systems:

Computing g(x,y) requires the computation of two direct Fourier transforms (applied to the image f(x,y) and to the filter response) and of the reverse transform applied to the product G(x,y) .

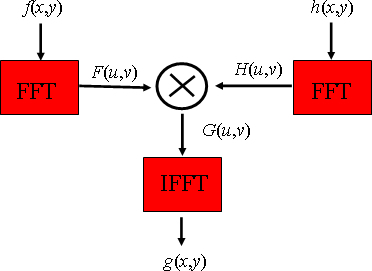
This computation scheme is efficient if the Fourier transforms are computation-optimized: we then talk about Fast Fourier Transforms (FFT). The detailed study of the FFTs falls outside of the scope of this lesson; however, the reader can find additional information on FFTs in reference [ [1] Traitement numérique du signal, théorie et pratique] .