Junction under small-signal AC voltage , diffusion capacitance

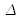Let's consider the case where the bias applied to the diode consists of a DC direct voltage V0>0 superimposed with a small-signal AC component with a weak amplitude V , at frequency f. The ohmic resistance of the doped semi-conductors is neglected (regime of weak injection.) This voltage creates a current which can be written as a combination of a DC current J0 and a AC current of amplitude J (at the same frequency), provided that a linear approximation of the J-V characteristic can be done around the (V0 , J0) point.

And

Where is the modulation angular frequency.

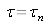For low modulation frequencies such as where or 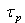is the carrier lifetime, the complex admittance 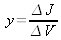is :

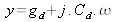with :

Where gd is the diffusion conductance , Cd is the diffusion capacitance.

This expression shows that the amplitude of the AC component varies exponentially with the DC component. Furthermore, there is a phase shift between the AC voltage and the AC current, modelled by a diffusion capacitor. This capacitance is due to the high finite mobility of carriers. Indeed, electrons and holes have a nonzero effective mass (which depends on the nature of the crystal: for instance in GaAs me=0.06.10-30kg); under the AC voltage, due to their quite high mobility they can reach reasonably high velocities. When the voltage is reversed rapidly the carriers cannot respond instantaneously to the driving voltage because of their mass or inertia. Therefore the total generated current is phase shifted with respect to the voltage.

For higher modulation frequencies such as 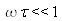, the complex admittance becomes :

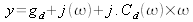with :