Equations of fiber holograms

We consider an opaque object, noted located at a distance from the CCD sensor, as shown in figure 8. According to Huygens integral and following Fresnel approximation, the amplitude of the complex field, noted ) is given by:

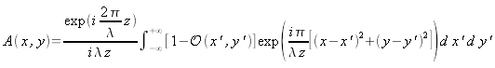
In the particular case where the transmittance of the object is expressed by a one-dimension function, equation (3.1) is expressed in a simplified form:

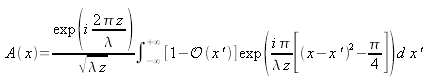
For an opaque fiber of diameter d centered in the origin, the transmittance of such an object is defined by the following equation:

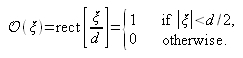
The complex field ) is expressed using first and second level Fresnel integrals:

where and . and are first and second level Fresnel integrals. Their definition is:

In the far field approximation, i.e. when , the intensity distribution is expressed by the following equation:

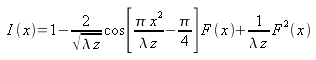
Figure 9 gives an example of intensity distribution.

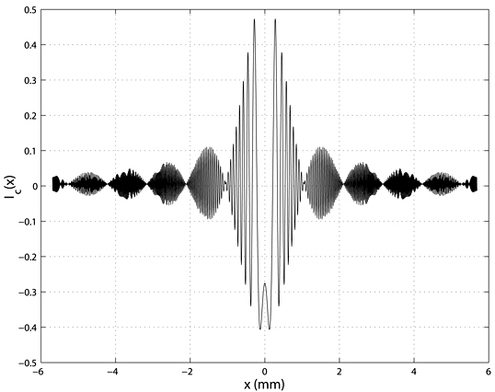
* Figure 9: Representation of the intensity distribution for and .

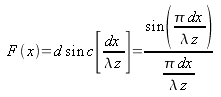
The expression is the Fourier transform of . As shown in equation (3.6), IntensityI(x) is partially described by a real linear chirped function:

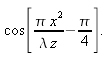
We will show that it is possible to analyze this type of signal by fractional FTs. As far field approximations are less restrictive than near-field approximations, we first focus on equation (3.6). The results remain valid in the near field.

As noted in the lesson or the previous chapter, the most important property of fractional Fourier transforms is that which connects them to Wigner distribution functions. Therefore, in the following paragraph, we will first examine the Wigner distribution function of the second term of equation (3.6).

We should keep in mind that Wigner distribution functions are defined by the integral form:

We shall examine the case of a function defined by:

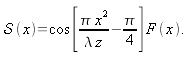
The function is the sum of two exponential terms:

with:

Wigner distributions are bilinear. Therefore, a nonlinear term will appear (called interferences) in the case of a multi-component signal. The Wigner distribution of (3.10) is finally:

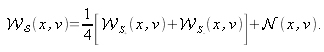
Using the method of stationary phases, the development of a nonlinear term, noted , gives the following result:

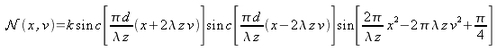
with . We clearly see that interference terms contain all information related to the system, that is to say the information about the axial position and the diameter of the fiber.

However, a study on this part of the signal does not seem trivial to describe diffraction patterns.

Therefore, we focus on the first two terms of equation (3.13).

Considering that is the Fourier transform of and that relations (2.32), (2.33) and (2.34) of the first lesson on the bases of fractional FTs and their properties to Wigner distributions, the first two terms of equation (3.13) can be written as the sum of the following Wigner distributions:

where:

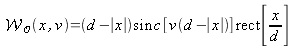
is the distribution function of the rectangular function defined by (3.3).

Figure 10 illustrates the Wigner distribution of .

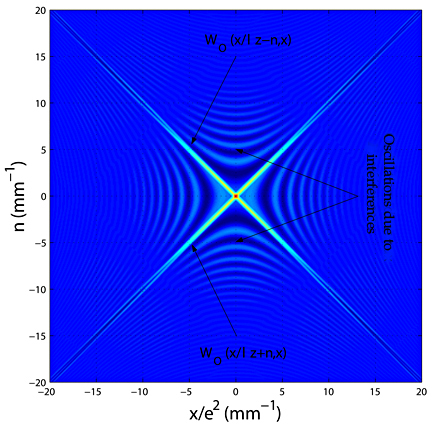
* Figure 10: Representation of the Wigner distribution of for and is the number of samples and the sampling interval.

In this example, the distance chosen equals to 100mm and the diameter d equals to 60μm.

This graph indicates the two distributions and and also the four external interference zones linked to the bilinearity of the operator.

The two branches of distribution are centered on variation laws .

Wigner distribution keeps the opening of the function on which it is applied.

Therefore the width of every branch corresponds to the diameter d of the opening of the rectangular function .

The intensity distribution (equation (3.6)) was traced in figure 9. In this case, the constant was removed.

This operation allows us to clearly indicate the Wigner distribution of the useful signal.

In fact, in Wigner space, a constant is translated by a Dirac pulse which prevents any signal description.

The representation in figure 9 is associated with its representation in Wigner space noted (figure 11).

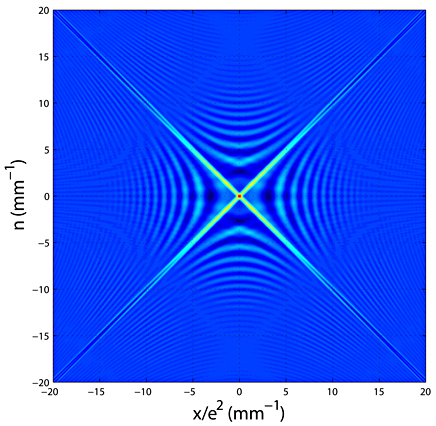
* Figure 11: Representation of the Wigner distribution of , noted for and .

We can note the effects of the autocorrelation term of the function on the interference terms.

Given the relation linking Wigner distribution functions with fractional Fourier transforms, we shall use this transform to restitute fiber holograms.