Qualité spatiale du faisceau laser en sortie

La cavité laser est d'abord un filtre spatial sélectionnant uniquement les rayons lumineux qui sont très proches de l'axe de la cavité : les autres sont perdus à cause de l'éloignement progressif de l'axe et de la dimension finie des miroirs (figure 8).

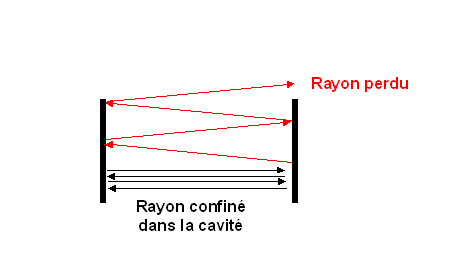
On constate qu'un laser fonctionnant à l'état stationnaire produit une onde lumineuse dont la structure spatiale ne varie pas dans le temps, et ce, malgré les nombreux allers et retour dans la cavité. Dans ce cas la cavité laser doit forcément admettre une onde lumineuse capable de se propager dans la cavité en revenant identique à elle-même en chaque point de la cavité après un aller et retour. Cette onde peut exister sous certaines conditions, c'est en général une onde dite “gaussienne”, dont la répartition d'éclairement a une forme gaussienne dans un plan perpendiculaire à l'axe de propagation. Physiquement, l'onde gaussienne concentre la lumière sur l'axe de la cavité. Une onde gaussienne qui se propage dans l'espace ressemble à un pinceau de lumière : on parle de faisceau gaussien. En mettant un carton ou un détecteur dans un plan perpendiculaire à l'axe de propagation de l'onde (en sortie du laser), on peut mesurer son éclairement en tout point (c'est à dire le nombre de photons par seconde passant par unité de surface). Cet éclairement a une forme gaussienne dans ce plan (figure 9).

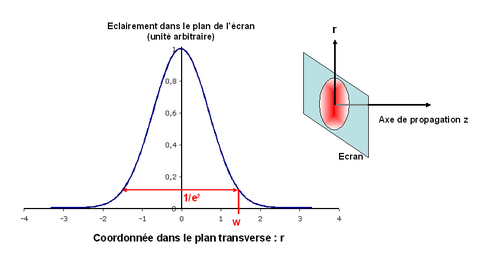
On peut définir dans ce plan une certaine extension spatiale de l'onde lumineuse. Le rayon du faisceau dans ce plan est par définition la distance entre l'axe optique et l'endroit où l'éclairement est divisé par 1/e2 par rapport au maximum d'éclairement de l'onde. On l'appelle w.

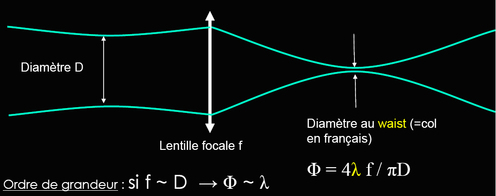
Une onde gaussienne se propage d'une façon un peu particulière qui ne ressemble pas tout à fait à une propagation au sens de l'optique géométrique. Elle admet une taille minimale w0 en un plan particulier (cet endroit est appelé le col du faisceau ou waist en anglais) (figure 10). Puis très loin du col, elle diverge “en ligne droite” avec un angle de divergence θ. Ces deux grandeurs sont liées par la relation suivante :

Pour un laser hélium néon par exemple, le rayon du faisceau dans le plan du col est de 1mm environ. Ceci correspond à une divergence très faible de 0,2mrad (il faut se propager sur 5m à partir du col pour que le rayon du faisceau ait doublé ! ). Il est impossible d'avoir de telles propriétés avec de la lumière issue de lampes classiques.

La formule ci-dessus exprime également le fait que si la divergence du faisceau est grande (par exemple avec une lentille utilisée pour focaliser le faisceau) le rayon du faisceau dans le plan du col est très petit. En général, il est possible de focaliser un faisceau laser sur un rayon de l'ordre de la longueur d'onde. Cela pourrait être fait également avec une lampe classique mais la différence est le nombre de photons qu'il est possible d'apporter par seconde sur une petite surface. Il est très faible pour une lampe classique alors qu'il est considérable pour un laser. Par exemple, un faisceau à 633 nm transportant une puissance lumineuse de 1mW correspond à un flux de 1015 photons par seconde et ce faisceau peut être facilement focalisé sur une tache d'un rayon de l'ordre du micromètre (figure 11). Ainsi, la densité de puissance d'un simple laser hélium néon en un point de focalisation peut largement dépasser celle qui serait donnée par l'image du soleil focalisé par une lentille.

Pour résumer, parmi tous les photons spontanés émis au départ par la “lampe-milieu amplificateur”, la cavité sélectionne un pinceau de lumière particulier (une onde gaussienne) et le nombre de photons portés par ce pinceau est rendu considérable par le processus d'émission stimulée existant à chaque aller et retour. Ce faisceau peut avoir une divergence très faible. Il peut également être focalisé sur des surfaces très petites moyennant des optiques adaptées.