Stabilité de la cavité
Écrivons la matrice ABCD sur un aller retour :
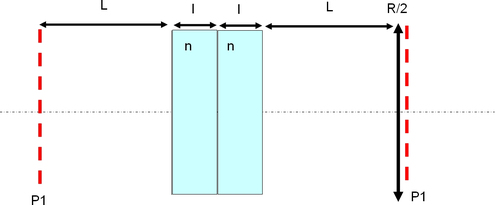
en observant la figure 2, le trajet aller-retour se décompose en :
-
le parcours d'une distance L dans l'air
-
le parcours d'une distance l dans le cristal d'indice n
-
la réflexion sur un miroir plan, qui n'a aucune incidence
-
à nouveau les parcours sur la distance l dans le cristal puis L dans l'air
-
enfin la réflexion sur le miroir de rayon de courbure R.
![[zoom...]](javascript:window.open(%22../res/Fig2_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
La cavité dépliée est représentée sur la figure 3 et correspond à la suite de matrices suivantes (attention à l'ordre !)
![[zoom...]](javascript:window.open(%22../res/fig3_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
En posant d = L + l/n pour alléger les notations, on trouve après calcul :
Pour que la cavité soit stable, il faut que
ce qui se résume ici à :
, soit une simple condition à vérifier (puisque d/R est évidemment positif) :
soit en reprenant les notations de base
Pour une cavité « vide », sans cristal, de longueur Leq, la condition de stabilité se serait écrite (voir cours) :
or
car Rplan est infini (miroir plan), donc la condition devient
ou encore
.
La cavité avec le cristal est donc équivalente du point de vue de la stabilité à une cavité vide de longueur équivalente
.
Il est facile de se tromper en prenant comme longueur équivalente la longueur optique L+nl !
Revenons à notre cavité : on peut donc choisir n'importe quel couple (rayon de courbure R – Distance L) vérifiant la condition
. En pratique, on verra que d'autres considérations, comme la taille souhaitée du waist dans la cavité, peuvent influer sur ces choix. De plus, on ne dispose pas concrètement d'un nombre illimité de miroirs de rayons de courbures différents !
Pour l'instant, prenons dans les tiroirs du laboratoire un miroir de rayon R = 100 mm.
La longueur L doit donc être inférieure à 100-10/1,8 ≈ 94,5 mm.
On prendra pour fixer les idées dans la suite L = 80 mm.