Structure du faisceau dans la cavité

Maintenant que les dimensions permettant de stabiliser la cavité ont été choisies, regardons de plus près à quoi va ressembler le faisceau dans la cavité.

On sait déjà que le waist va se situer au niveau du miroir plan, puisque le faisceau doit revenir sur lui-même.

Commençons par déterminer la taille des faisceaux sur les miroirs, que l'on notera w0 sur le miroir plan et w1 sur le miroir sphérique, ainsi que la divergence et la longueur de Rayleigh ZR associées :

On va raisonner pour simplifier sur la cavité équivalente de longueur .

En prenant z=0 au niveau du miroir plan, on peut écrire qu'en z = d, c'est à dire sur le miroir sphérique, le rayon de courbure du faisceau laser doit être le même que celui du miroir (toujours pour assurer un retour sur lui-même du faisceau). Or on connaît la loi de variation de R avec z (voir cours), ce qui nous amène à écrire :

on en déduit facilement

avec d = L+l/n = 80+10/1,8 = 85,5 mm et R = 100 mm il vient :

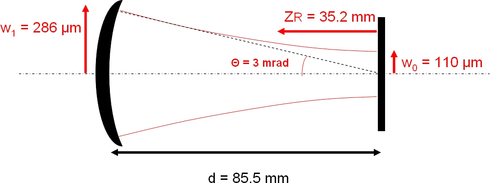
ZR = 35,2 mm et w0 = 110 µm (la longueur d'onde vaut 1064 nm)

La divergence vaut soit 3 mrad.

Pour connaître le rayon du faisceau sur le miroir sphérique, on applique simplement la formule suivante :

ce qui nous donne en z=d :

soit numériquement w1 = 286 µm.

La structure du faisceau dans la cavité est donc la suivante (figure 4) :