Le filtre adapté

Le concept de filtre adapté joue un rôle important dans les problèmes de reconnaissance des caractères.

Si on applique un signal d'entrée g(x, y) à un filtre adapté à s(x, y), on trouve un signal de sortie v(x, y) de la forme :

où l'on reconnaît le produit d'intercorrélation des fonctions g et s.

Historiquement, la notion de filtre adapté est d'abord apparue dans le domaine de la détection des signaux; si on a à détecter un signal de forme connue, noyé dans un bruit «blanc», l'utilisation d'un filtre adapté permet de réaliser une opération linéaire qui rend maximal le rapport de la puissance instantanée du signal (à un instant donné) à la puissance moyenne du bruit. Cependant, dans l'application présente, les caractères seront supposés ne pas contenir de bruit, et l'utilisation d'un mode particulier de filtrage se justifie différemment.

L'interprétation optique donnée par la figure EC1 permet de mieux comprendre le mécanisme du filtrage adapté.

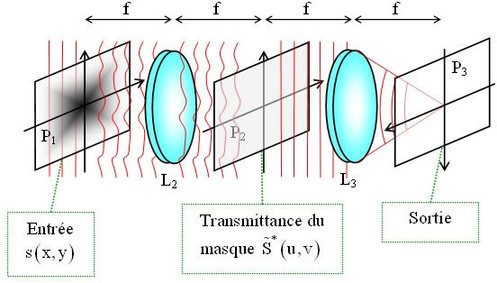
Supposons que l'on ait à réaliser un filtre adapté au signal d'entrée s(x, y) au moyen d'un masque fréquentiel disposé dans le plan spectral d'un système classique de traitement cohérent. La transformation de Fourier de la réponse impulsionnelle (Eq. (1)) montre que la fonction de transfert nécessaire est :

Où et . Le masque fréquentiel doit donc avoir une transmittance en amplitude proportionnelle à .

Considérons à présent la nature particulière de l'amplitude de l'onde transmise par le masque lorsqu'on applique le signal s (auquel le filtre est adapté) à l'entrée du système. Ce masque reçoit une amplitude complexe proportionnelle à et transmet une distribution proportionnelle à . Cette dernière quantité est réelle, ce qui implique que le masque fréquentiel compense exactement la courbure de l'onde incidente . L'amplitude complexe transmise représente donc une onde plane que la dernière lentille du système transforme en une tache brillante dans le plan de sortie du système. Lorsqu'on applique un signal d'entrée autre que s(x, y), la courbure de l'onde n'est pas, en général, compensée par le masque fréquentiel et la lumière transmise n'est plus concentrée en une tache brillante par la dernière lentille. On conçoit alors qu'on puisse détecter la présence du signal s en mesurant l'intensité lumineuse dans le plan focal de la dernière lentille du système. (Si le signal d'entrée s n'est pas centré à l'origine, la tache brillante dans le plan de sortie se déplace d'une distance égale à la distance du centre du signal s à l'axe).