Exemple de problème de reconnaissance de caractères.
Considérons le problème particulier suivant : le signal d'entrée g du système de traitement est constitué par l'un quelconque de N caractères possibles s1 , s2 ... sN et on se propose de déterminer lequel de ces caractères constitue effectivement le signal g. Comme nous allons le montrer, le processus d'identification peut être réalisé en appliquant le signal d'entrée à une série de N filtres, chacun d'eux étant adapté à l'un des caractères pouvant constituer le signal d'entrée (voir figure EC2).
![[zoom...]](javascript:window.open(%22../res/image_ec_02_1.jpg%22,%22_blank%22,%22width=%22+Math.min(800,screen.availWidth)+%22,height=%22+Math.min(600,screen.availWidth)+%22,left=%22+(screen.availWidth-800)/2+%22,top=%22+(screen.availHeight-600)/2+%22,scrollbars=yes,resizable=yes%22)?void(0):void(0)){kind=link}
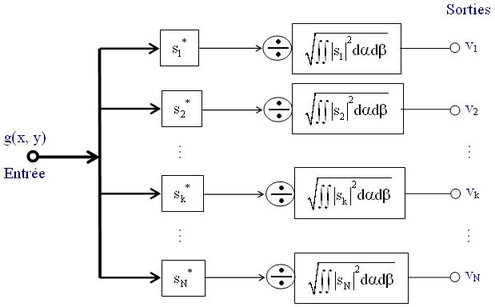
La figure EC2 représente un schéma-bloc d'un dispositif de reconnaissance. Le signal d'entrée est appliqué simultanément (ou successivement) aux N filtres adaptés de fonctions de transfert
,
...
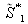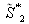. La réponse à chacun des filtres est normalisée par la racine carrée de l'énergie totale correspondant au caractère auquel il est adapté. Cette normalisation, qui peut être réalisée par voie électronique après détection des signaux sortant des filtres, tient compte du fait que les divers caractères servant de signal d'entrée ne laissent généralement pas passer la même énergie. Enfin, on compare les carrés des modules des signaux de sortie
,
, ...,
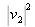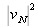en chacun des points où on pense trouver les maxima des signaux de sortie (on suppose ainsi que le caractère auquel ils sont adaptés est présent dans chaque cas). Nous allons montrer maintenant que, si le caractère particulier sk. est effectivement présent dans le signal d'entrée, c'est-à-dire si ,
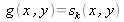la valeur
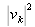correspondante est la plus élevée des N réponses.
En effet, notons d'abord que, d'après l'Eq. (2), le maximum du signal de sortie vk du filtre adapté qui convient est donné par:
D'autre part, la réponse
avec
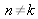, d'un filtre adapté à un caractère différent de
est donnée par:
En utilisant l'inégalité de Schwarz, nous pouvons écrire:
On en déduit aisément:
l'égalité étant réalisée si et seulement si:
Ce résultat montre donc que le filtre adapté fournit un moyen de reconnaître, parmi un lot de caractères possibles, lequel est réellement présenté au système.