Lame de verre

Le système interférométrique à division de front d'onde le plus simple est donné par une lame de verre ou un coin de verre observé en réflexion. Ce paragraphe est fortement inspiré du Chapitre 6 de la référence [].

Lors de la réfraction sur un dioptre du type air-verre, environ 4% de l'énergie lumineuse est réfléchie. La lumière ainsi réfléchie ou transmise peut être à l'origine d'un phénomène d'interférences. Dans ce paragraphe on ne considèrera que les interférences par réflexion, le cas de la transmission étant similaire. Une source étendue et monochromatique située dans l'air éclaire une lame à faces parallèles d'indice , d'épaisseur  (figure 5) posée sur un troisième milieu d'indice . La source étant étendue on recherche la zone de localisation des franges d'interférences.

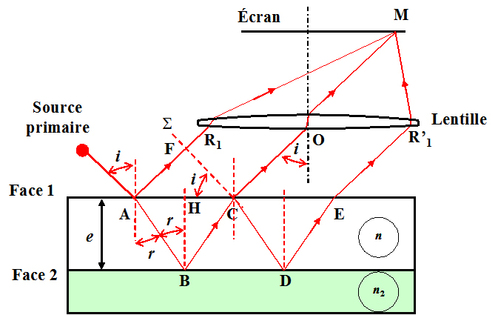
Le rayon incident issu de la source primaire se réfléchit partiellement en suivant la direction tandis qu'une partie du rayon réfracté est réfléchie suivant puis réfracté à nouveau dans la direction . Les contributions du rayon et des suivants sont négligées car l'énergie lumineuse de ces rayons décroît très rapidement. En effet si l'énergie lumineuse est de 4% pour le premier rayon réfléchi , elle n'est plus que de 0,0059 % pour le troisième rayon . Les deux rayons et issus du même rayon incident , émergent parallèlement entre eux, ils « interfèrent à l'infini ». Si un écran est situé dans le plan focal image d'une lentille convergente les rayons émergents de la lentille se croisent en , la figure d'interférences est alors projetée sur l'écran.

Comme dans le cas des fentes d'Young, on peut exprimer la différence de marche  en fonction des caractéristiques du dispositif interférentiel, c'est à dire de la lame, ainsi que la forme géométrique des franges d'interférences.

Le rayon incident donne deux rayons réfléchis et . Au-delà des points et les deux rayons réfléchis parcourent le même chemin optique. En revanche, entre et le rayon parcourt la distance dans l'air et le rayon parcourt le chemin dans le milieu d'indice . La différence de chemin optique entre ces deux rayons et est égale à :

Considérons le triangle  :

d'où :

Soit en appliquant la loi de Descartes pour la réfraction en  :

Pour le triangle nous avons les deux relations trigonométriques suivantes :

soit :

et :

soit :

En remplaçant , et par leurs expressions en fonction de , et dans la première équation :

Deux cas sont à considérer :

• si les indices sont tels que :

les deux réflexions en et en sont du même type, c'est à dire qu'à chaque fois la réflexion a lieu d'un milieu moins réfringent sur un milieu plus réfringent. La différence de marche  est alors égale à la différence de chemin optique :

• si les indices sont tels que :

Les réflexions ne sont pas du même type, on admettra qu'il faut dans ce cas ajouter à la différence de chemin optique pour obtenir la différence de marche [] :

L'ensemble des points pour lesquels la différence de marche est la même sont dans le même état d'interférence. L'aspect géométrique des franges d'interférences est donné par la recherche des conditions pour lesquelles .

Dans le cas des franges lumineuses, les interférences sont constructives, la différence de marche  est égal à un nombre entier de fois la longueur d'onde (voir le cours « Interférences  : Fonfamentaux » :

Pour un dispositif donné, la longueur d'onde, l'indice et l'épaisseur de la lame sont des constantes, les points dans le même état d'interférence vérifient :

Les angles de réfraction et d'incidence étant relié par la loi de Descartes, ceci conduit à . L'observation de la figure d'interférences sur un écran situé dans le plan focal image de la lentille montre des anneaux concentriques alternativement brillants et sombres (figure 6).

On s'intéresse maintenant aux rayons angulaires des anneaux d'égale inclinaison pour une épaisseur de la lame. On se place dans le cas où le centre des anneaux est brillant. Au centre, la différence de marche notée correspond à un angle de réfraction nul, elle est égal à un nombre impair de fois la demi longueur d'onde :

dans le cas où :

Pour les anneaux périphériques noirs, augmente, la différence de marche est inférieure à et :

L'écart de la différence de marche entre un anneau noir périphérique d'ordre et l'anneau central est égal à :

et avec un développement limité du cosinus pour les petits angles  :

d'où :

La loi de Descartes appliquée aux petits angles permet d'en déduire l'angle d'incidence  :

Dans l'air et pour des angles faibles, l'interfrange a pour expression :