Interféromètre de Michelson

Dans sa version la plus simple, l'interféromètre de Michelson est composé d'une source de lumière, de deux miroirs plans réfléchissants, d'une lame semi-réfléchissante et d'un écran. La figure 9 décrit le dispositif expérimental. Le miroir 1 est situé à la distance de la lame et le miroir 2 à la distance . Suivant les deux trajets, on a deux systèmes optiques qui jouent le rôle de miroir. Pour le trajet n°1 : séparatrice puis le miroir . Donc la source 1, image de la source primaire , est donnée par le symétrique de par rapport à la séparatrice puis par le symétrique par rapport à . La démarche est identique sur le trajet n°2 avec le miroir , puis la lame séparatrice.

Le dispositif est donc équivalent à un système de trous d'Young comme il est décrit sur la figure 10.

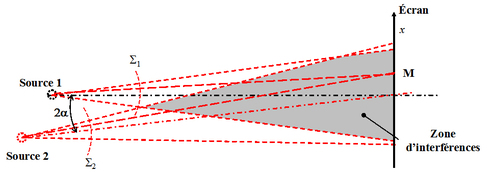
Les miroirs ne sont pas nécessairement situés à la même distance de la lame et les sources secondaires de la géométrie équivalente ne sont pas nécessairement dans le même plan ni sur le même axe. Si le miroir 2 par exemple est basculé d'un angle par rapport à l'axe optique, les deux sources secondaires sont également décalées. On se retrouve dans la configuration décrite au paragraphe I.B.6 du cours « Interférences : Fondamentaux ». Pour tout point de l'écran de coordonnées , la phase des interférences est

Les franges observées sont celles décrites sur la figure 6 du cours « Interférences : Fondamentaux ».

L'interféromètre de Michelson peut également être configuré pour fonctionner avec des ondes planes. Dans ce cas, il suffit de collimater l'onde initiale au moyen d'un objectif : on place la source au foyer d'une lentille et les miroirs sont éclairés en lumière parallèle donc en ondes planes. La figure 11 schématise le montage.

On se retrouve dans le cas du paragraphe I.B.5 du cours « Interférences : Fondamentaux ». Les inclinaisons des miroirs 1 et 2 donnent les orientations des vecteurs d'ondes des deux ondes planes secondaires. Considérons que le miroir 1 est perpendiculaire à l'axe optique et que le miroir 2 est basculé d'un angle suivant et suivant . Les vecteurs d'ondes s'écrivent

Dans le plan , les pentes de la surface d'onde sont et . En tout point de l'écran, la phase des interférences est donnée par :

et le signal d'interférences s'écrit :

L'interfrange suivant est donnée par :

et l'interfrange suivant est donnée par :

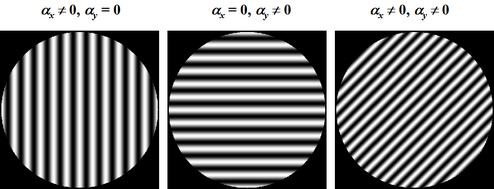
La figure 12 montre le champ spatial d'interférences dans la zone de superposition des deux ondes en fonction de l'inclinaison du miroir 2 dans les deux directions et (soient et ).